Next: Lagrange Multiplier Up: Conditional Extrema Previous: Conditional Extrema Contents Index
From the equation
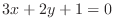 , we can find
, we can find 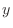 in terms of
in terms of 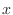 . In other words, we can find
. In other words, we can find
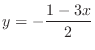 . In general, given a quadratic function
. In general, given a quadratic function 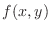 , if
, if 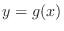 always satisfies
always satisfies
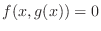 , then we say the equation
, then we say the equation 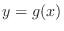 is an implicit function determined by the equation
is an implicit function determined by the equation
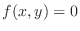 .
.
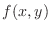 is the class
is the class 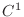 at
at
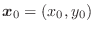 in the region
in the region  . If
. If
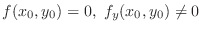
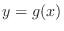 determined by
determined by
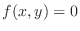 in the neighborhood of
in the neighborhood of 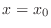 which satisfies
which satisfies
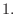 |
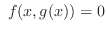 |
||
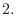 |
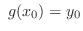 |
||
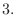 |
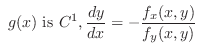 |
NOTE In the neighborhood of the point satisfying
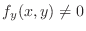 , the implicit function
, the implicit function 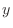 exists and the implcit function is differentiable. Thus the total diffetential of
exists and the implcit function is differentiable. Thus the total diffetential of 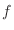 is
is
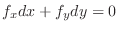
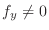 ,
,
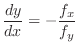
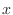 , we have
, we have
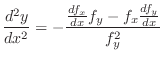
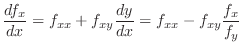
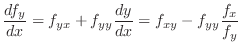
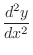 |
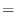 |
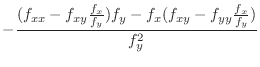 |
|
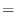 |
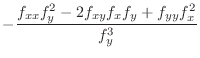 |
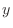 such as
such as
 deteremined by
deteremined by
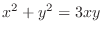
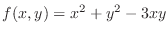 and take total differential of
and take total differential of 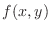 ,
,
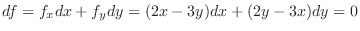
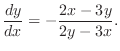
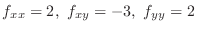 ,
,
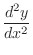 |
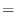 |
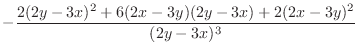 |
|
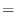 |
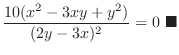 |
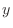 such as
such as
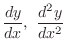 deteremined by
deteremined by
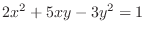
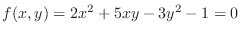 and find total differential of
and find total differential of 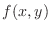 . Then
. Then
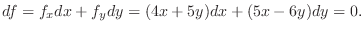
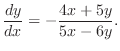
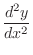 |
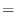 |
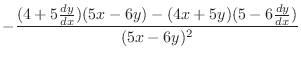 |
|
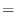 |
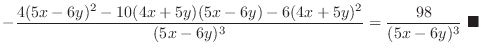 |
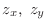 for the implicit function
for the implicit function
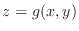 determined by the equation
determined by the equation
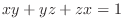 .
.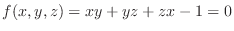 , set
, set
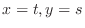 . Then,
. Then,
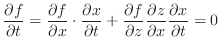
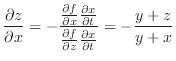
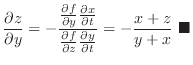
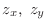 for the implicit function
for the implicit function
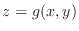 determined by the equation
determined by the equation
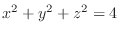 .
.
SOLUTION
For
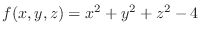 , set
, set
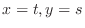 .
.
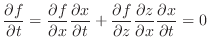
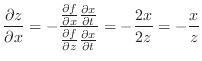
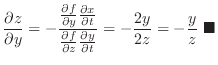
 of
of 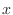 is determined by the equations
is determined by the equations
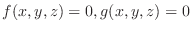 , then,
, then,
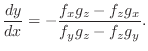
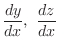 for the implicit functions
for the implicit functions 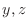 of
of 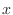 determined by the equations
determined by the equations
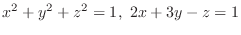 .
.
SOLUTION
Let
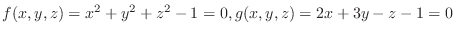 . Then totally differentiate
. Then totally differentiate 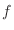 and
and 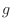 to get
to get
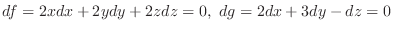
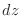 to get
to get
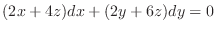
Thus,
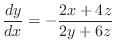
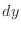 to get
to get
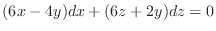
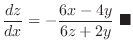
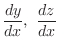 for the implicit functions
for the implicit functions 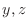 of
of 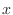 determined by the equations
determined by the equations
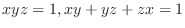 .
.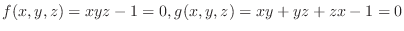 . Then find total derivatives.
. Then find total derivatives.
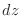 .
.
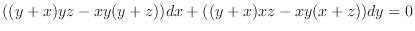
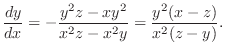
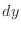 .
.
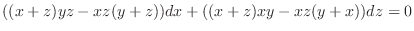
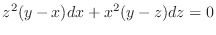
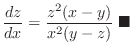
Exercise A
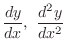 for the implicit functions
for the implicit functions 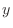 of
of 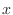 determined by the following functionsD
determined by the following functionsD
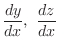 for the implicit functions
for the implicit functions 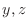 of
of 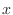 determined by the following functionsD
determined by the following functionsD
Exercise B
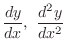 for the implicit function
for the implicit function 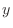 of
of 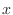 determined by the following equations.
determined by the following equations.
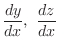 for the implicit function
for the implicit function 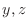 of
of 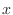 determined by the following equations.
determined by the following equations.
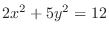 at the point
at the point
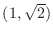 .
.
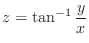 at the point
at the point
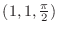 DFind the equation of the normal line through
DFind the equation of the normal line through
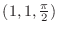 .
.
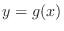 implicitly defined by the following equationsD
implicitly defined by the following equationsD