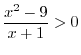Next: Functions Up: Introduction Previous: Inequalities Contents Index
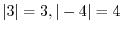 is given by
is given by
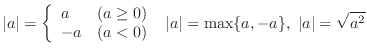
We first consider the inequality
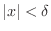
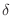 is some positive number. Now
is some positive number. Now
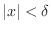 can be thought of the points on the number line whose distance from the origin is less than
can be thought of the points on the number line whose distance from the origin is less than 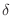 . Thus,
. Thus,
\colorbox{calc-color}{ \begin{minipage}{13.35cm} \begin{equation} |x| < \delta \Leftrightarrow -\delta < x < \delta \label{eq:ineq1-1} \end{equation} \end{minipage} }
Next?C
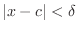 can be thought of the points whose distance from the point
can be thought of the points whose distance from the point 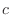 is less than
is less than 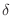 . Thus,
. Thus,
Lastly?C
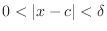 can be thought of
can be thought of
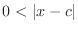 and
and
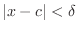 ?DThe first inequality is
?DThe first inequality is  . Thus?C
. Thus?C
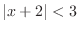
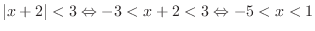
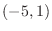

Let
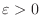 . Then
. Then
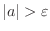 can be think of the distance from the origin to
can be think of the distance from the origin to 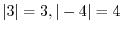 is larger than
is larger than
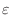 ?DThus?C
?DThus?C
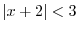
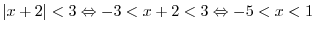
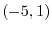 . Thus
. Thus 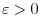 . By the second inequality?Cwe have
. By the second inequality?Cwe have 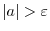 . Thus
. Thus 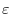 ?DFrom this, the solution is
?DFrom this, the solution is
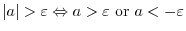

One of the popular inequalities of calculus is the triangle inequality?D
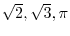 ,
,
|
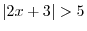
|
PROOF If you think of 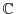 as
as
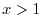 , then the proof is easy. Note that
, then the proof is easy. Note that
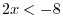
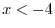
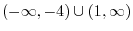

Here is another inequality used in calculus.
|
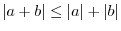
|
|
Exercise A
|
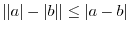
 ?C
?C