Next: ANSWERS Up: Application of Definite Integrals Previous: Volume Contents Index
| arc length |
|---|
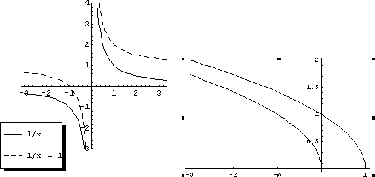
Let 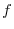 be class be class 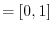 . Then the arc length . Then the arc length 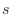 of a curve of a curve 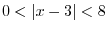 , where , where
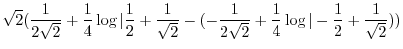 is given by is given by
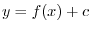
|
![$[a,b]$](img1084.png)
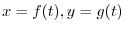
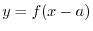 be the point
be the point
 . Then connect the points
. Then connect the points
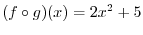 by a straight line to get
by a straight line to get
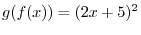
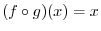 .
.
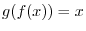
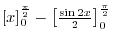 get smaller, if the Riemann sum converges to
get smaller, if the Riemann sum converges to 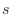 , then we say
, then we say  arc length of
arc length of 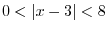 for
for
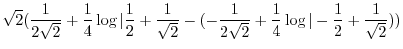 .
.
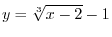

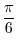

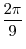
Note that since 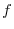 is the class
is the class 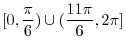 , use the mean value theorem,
, use the mean value theorem,
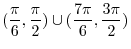
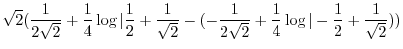 is
is
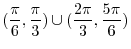
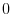
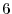 . Then the small arc length
. Then the small arc length 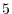 is given by
is given by
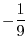
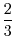 . Thus
. Thus
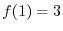 |
 |
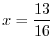 |
|
 |
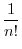 |
||
 |
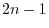 |
||
 |
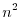 |
||
 |
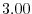 |
||
 |
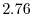 |
||
 |
![$\displaystyle 12 \int_0^1 udu = 12 \left[\frac{u^2}{2}\right]_0^1 = 12\cdot \frac{1}{2} = 6\ensuremath{\ \blacksquare}$](img3490.png) |
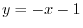
SOLUTION Parametrize by
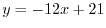 .
.
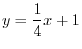
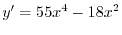

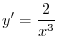

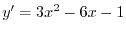

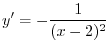

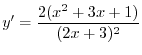

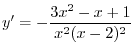
Now let
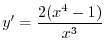 . Then
. Then
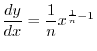 and
and
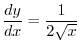
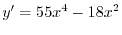 |
 |
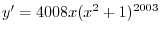 |
|
 |
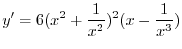 |
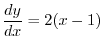 . Then
. Then 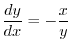 and
and
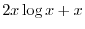
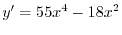 |
 |
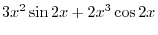 |
Now use the following integral formula,
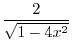
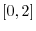 . Then
. Then
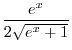 . Also,
. Also,
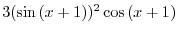 ,
,
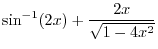
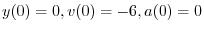 |
 |
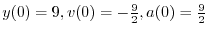 |
|
 |
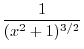 |
||
 |
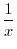 |
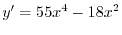

![$\displaystyle 2\sqrt{2}\cdot \frac{1}{2}\left[(w\sqrt{w^2 + \frac{1}{4}} + \frac{1}{4}\log\vert w + \sqrt{w^2 + \frac{1}{4}}\vert)\right]\mid_{-1/2}^{1/2}$](img3528.png)

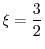

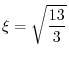

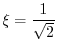
|
Exercise A
|
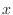 -axis?D
-axis?D
(a)
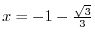 from
from 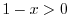 to
to  (b)
(b)
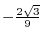 from
from 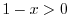 to
to 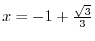 (c)
(c)
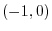 from
from 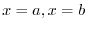 to
to
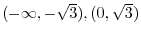
(d)
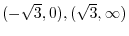 from
from
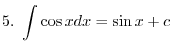 to
to
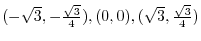
|
Exercise B
|
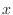 -axis?D
-axis?D
(b)
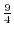 and
and 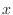 -axis?D
-axis?D