Next: Taylor's Theorem Up: Differentiation Previous: Mean Value Theorem Contents Index
| Indeterminate Form |
|---|
The following cases are indeterminate.
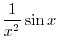
|
Proof
We consider a function which satisfies the conditions of Rolle's Theorem. Let
Cauchy's Mean Value Theorem
 and
and  be continuous on
be continuous on ![$[a,b]$](img1084.png) adn differentiable on
adn differentiable on  . If
. If
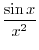 and
and
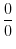 and
and
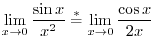 never takes 0 simultaneously, then there exists at leat one number
never takes 0 simultaneously, then there exists at leat one number
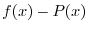 such that
such that
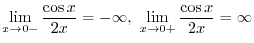
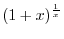
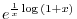 and
and 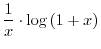 satisfies the conditions of Rolle's Theorem. Thus there exists at least one number
satisfies the conditions of Rolle's Theorem. Thus there exists at least one number
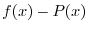 such that
such that
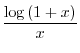
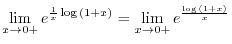
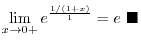 , then
, then
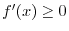 and this violates the assumption. Therefore,
and this violates the assumption. Therefore,
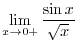 and
and
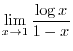
Proof
Let L'Hospital's Theorem
 and
and  be continuous on
be continuous on ![$[a,b]$](img1084.png) and differentiable on
and differentiable on 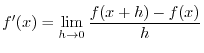 . If
. If
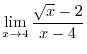 and
and
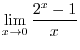 exists, then
exists, then
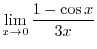 .
.  be such that
be such that 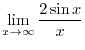 and consider
and consider
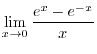
 such that
such that
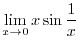
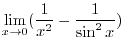
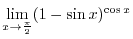
SOLUTION
This is indeterminate form of
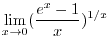 . Then differentiate the numerator and denominator separately, we have
. Then differentiate the numerator and denominator separately, we have
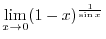
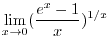 . So, differentiate the numerator and denominator separately, we have
. So, differentiate the numerator and denominator separately, we have
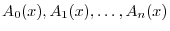
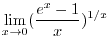 . So, differentiate the numerator and denominator separately, we have
. So, differentiate the numerator and denominator separately, we have
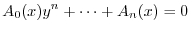

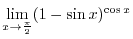 |
 |
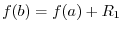 |
|
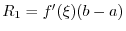 |
 |
||
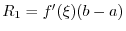 |
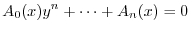 |
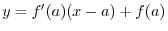
 . Then we replace
. Then we replace
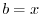 by
by
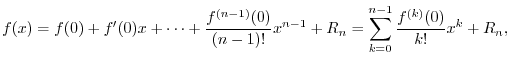 . Then it is indeterminat form of
. Then it is indeterminat form of
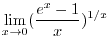 . Thus by L'Hospital's Theorem, we have
. Thus by L'Hospital's Theorem, we have
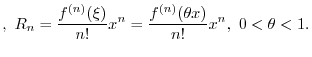
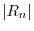 . Thus no limit exists
. Thus no limit exists

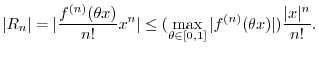
SOLUTION
This is indeterminate form of
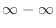 . Then replace
. Then replace
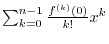 by
by
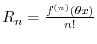 . Then it is indeterminate form of
. Then it is indeterminate form of
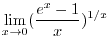 . Thus
. Thus
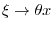
SOLUTION
This is indeterminate form of
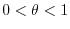 . So we rewrite
. So we rewrite
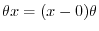 into
into
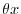 . Then
. Then
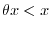 is indeterminate form of
is indeterminate form of
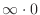 . Thus replace
. Thus replace
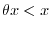 by
by
 . Then in the form of
. Then in the form of
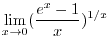 . Thus
. Thus
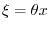 |
 |
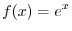 |
|
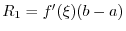 |
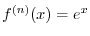 |
|
Exercise A
|
|
Exercise B
|