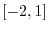Next: Properties of Continuous Functions Up: Functions Previous: One sided limit Contents Index
NOTE Suppose the domain of Continuous functions
Suppose  is a function defined on the interval
is a function defined on the interval
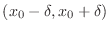 and satisfies the condition
and satisfies the condition
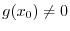
 is continous at
is continous at 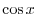 .
.
 contains the interval
contains the interval
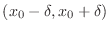 . Then
. Then  is continuous at
is continuous at 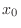 except the following two cases.
except the following two cases.
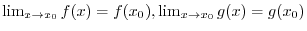 does not exist
does not exist
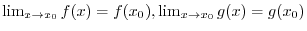 exists but not equal the value
exists but not equal the value 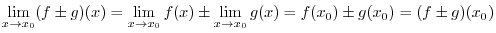
Case 1.  is called essentail discontinuity.
Case 2.
is called essentail discontinuity.
Case 2.  is called removal discontinuity. For this case, we can set a new value for
is called removal discontinuity. For this case, we can set a new value for 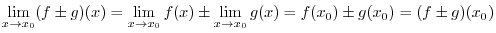 to make continuous.
to make continuous.
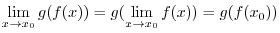 .
.
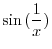 and
and 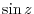 , we have
, we have
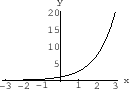
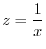 . Thus
. Thus  is discontinuous
is discontinuous 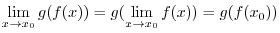 . The graph of function has a jump at
. The graph of function has a jump at 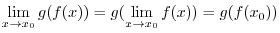

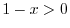 .
.
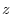
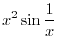 is bibrating, it should be squeezed by the absolute value.
is bibrating, it should be squeezed by the absolute value.
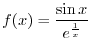
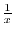 and
and
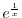 . Thus by the squeezing theorem, we have
. Thus by the squeezing theorem, we have
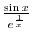
 , we have
, we have
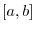
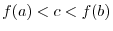 . Thus
. Thus  is continous at
is continous at 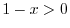

Continuous on an Interval
If  is continuous at every value in I, then we say
is continuous at every value in I, then we say  is continuous on I.
is continuous on I.
Proof
1.
Continuity Properties
 and
and 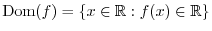 is continuous at
is continuous at 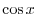 and
and 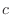 is a constant. Then
is a constant. Then
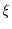 is continuous at
is continuous at 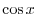
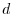 is continuous at
is continuous at 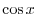
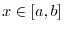 is continuous at
is continuous at 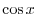
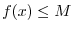 is continuous at
is continuous at 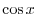 provided
provided
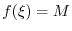
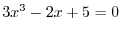 , Thus
, Thus
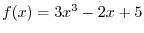

Proof
Composite Continuous Functions
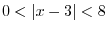 is continuous at
is continuous at 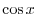 and
and  is continuous at
is continuous at
 . Then the composite function
. Then the composite function
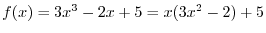 is Continuous at
is Continuous at 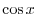 .
. 

As you can see, a continuous function is easy function to use.
 .
.
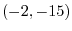
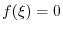 can be thought of a composite function of
can be thought of a composite function of 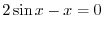 and
and
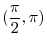 . Now
. Now 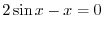 and
and
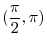 are continuous function of
are continuous function of 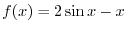 and
and 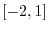 . Thus
. Thus
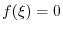 is continuous at
is continuous at 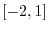 . Also
. Also 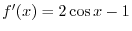 is continuous on
is continuous on
 . By 1.9, for
. By 1.9, for 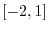
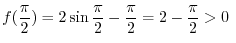 is continuous
is continuous

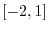 .
.
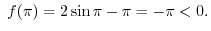
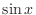 is continuous on
is continuous on
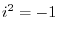 and
and 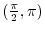 is continuous on
is continuous on
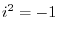 . Note that
. Note that
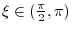 is continuous on
is continuous on 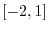 . Thus,
. Thus,
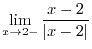 is continuous on
is continuous on 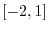 . Finally, a produnct of continuous functions is continuous, we have
. Finally, a produnct of continuous functions is continuous, we have
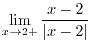 is continuous on
is continuous on