Next: Improper integrals Up: MULTIPLE INTEGRATION Previous: Change of variables 索引
7.3
1. The region of integration is a circle, ellipse, or rhombus. Then use the change of variables.
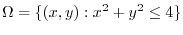
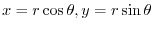 . Then
. Then
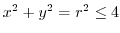 .Thus,
.Thus, 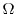 is maps to
is maps to
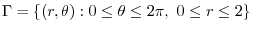
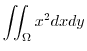 |
 |
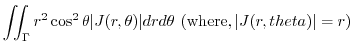 |
|
 |
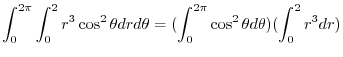 |
||
 |
![$\displaystyle \int_{0}^{2\pi}\frac{1 + \cos{2\theta}}{2} d\theta ([\frac{r^4}{4}]_{0}^{2} = \frac{1}{2}([\theta + \frac{\sin{2\theta}}{2}]_{0}^{2\pi})(4)$](img662.png) |
||
 |
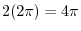 |
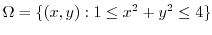
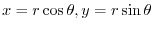 implies
implies
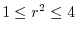 .Then
.Then 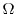 is maps to
is maps to
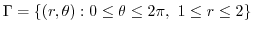
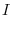 |
 |
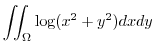 |
|
 |
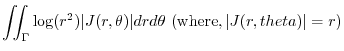 |
||
 |
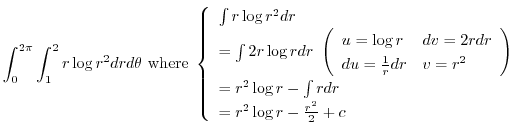 |
||
 |
![$\displaystyle 2\pi[r^2\log{r} - \frac{r^2}{2}]_{1}^{2} = 2\pi(4\log{2} - 2 + \frac{1}{2})$](img671.png) |
||
 |
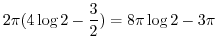 |
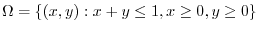
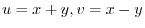 .
Since
.
Since
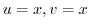 , a line
, a line 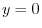 maps to
maps to 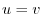 ,Also since
,Also since
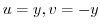 ,
, 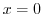 maps to
maps to 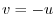 . Aline
. Aline 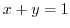 maps to
maps to
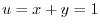 . Then
. Then
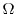 maps to
maps to
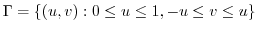
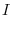 |
 |
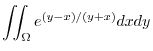 |
|
 |
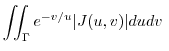 note that note that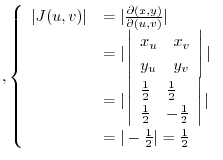 |
||
 |
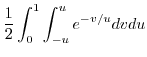 |
||
 |
![$\displaystyle \frac{1}{2}\int_{0}^{1}[-ue^{-v/u}]_{-u}^{u} du$](img685.png) |
||
 |
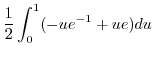 |
||
 |
![$\displaystyle \frac{1}{2}[-\frac{u^2}{2e} + \frac{u^2 e}{2}]_{0}^{1}$](img687.png) |
||
 |
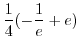 |
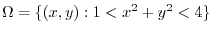
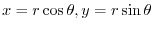 implies
implies
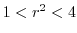 .Thus
.Thus 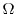 maps to
maps to
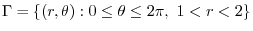
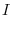 |
 |
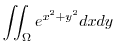 |
|
 |
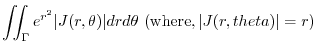 |
||
 |
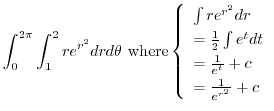 |
||
 |
![$\displaystyle (\int_{0}^{2\pi}\ d\theta)[\frac{1}{2}{e^{r^2}}]_{1}^{2}$](img695.png) |
||
 |
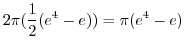 |
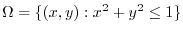
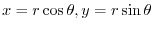 implies
implies
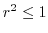 .Then
.Then 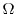 maps to
maps to
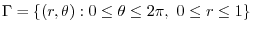
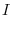 |
 |
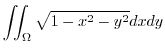 |
|
 |
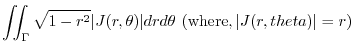 |
||
 |
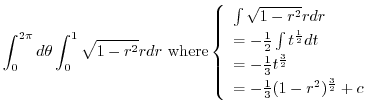 |
||
 |
![$\displaystyle 2\pi[-\frac{1}{3}(1 -r^2)^{\frac{3}{2}}]_{0}^{1}$](img703.png) |
||
 |
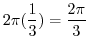 |
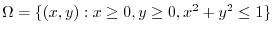
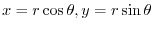 implies
implies
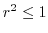 .Also,
.Also,
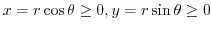 implies
implies
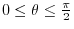 .Thus
.Thus 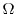 maps to
maps to
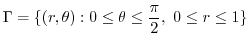
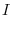 |
 |
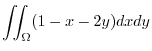 |
|
 |
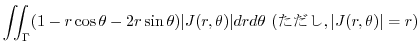 |
||
 |
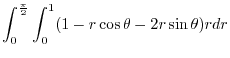 |
||
 |
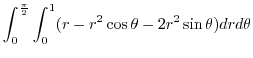 |
||
 |
![$\displaystyle \int_{0}^{\frac{\pi}{2}}([\frac{r^2}{2} - \frac{r^3 \cos{\theta}}{3} - \frac{2r^3 \sin{\theta}}{3}]_{0}^{1}) d\theta$](img713.png) |
||
 |
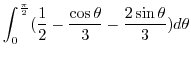 |
||
 |
![$\displaystyle [\frac{\theta}{2} - \frac{\sin{\theta}}{3} + \frac{2\cos{\theta}}{3}]_{0}^{\frac{\pi}{2}}$](img715.png) |
||
 |
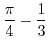 |
2.
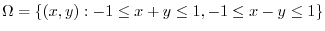
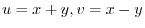 .
Aline
.
Aline 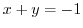 maps to
maps to 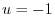 by
by 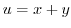 ,A line
,A line 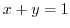 mpas to
mpas to
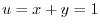 ,A line
,A line 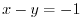 maps to
maps to 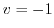 by
by 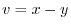 ,
A line
,
A line 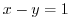 maps to
maps to
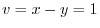 . Then
. Then
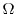 maps to
maps to
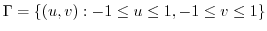
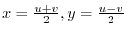 implies
implies
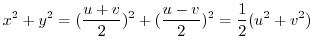
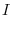 |
 |
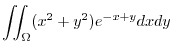 |
|
 |
 |
||
 |
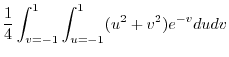 |
||
 |
![$\displaystyle \frac{1}{4}\int_{-1}^{1}[\frac{u^3}{3}e^{-v} + uv^2 e^{-v}]_{-1}^{1} dv$](img732.png) |
||
 |
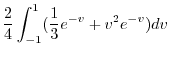 |
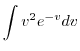 |
 |
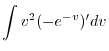 |
|
 |
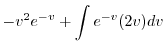 |
||
 |
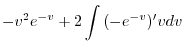 |
||
 |
![$\displaystyle -v^2 e^{-v} + 2[-e^{-v}v + \int{e^{-v}}dv]$](img738.png) |
||
 |
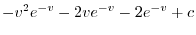 |
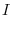 |
 |
![$\displaystyle \frac{1}{2}[-\frac{1}{3} e^{-v} - v^2 e^{-v} - 2v e^{-v} -2e^{-v}]_{-1}^{1}$](img740.png) |
|
 |
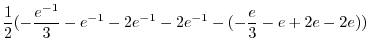 |
||
 |
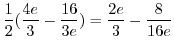 |