Next: Implicit functions Up: PARTIAL DIFFERENTIATION Previous: Extreme values 索引
6.7
1.
(a)
Since
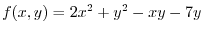 ,
,
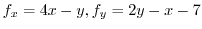 .
If
.
If 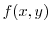 attains the extreme at
attains the extreme at
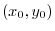
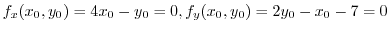
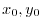 , we have
, we have
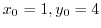 .
Next for
.
Next for
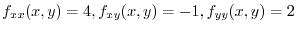 ,
,
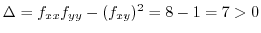 , we have
, we have
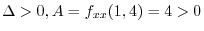 . Thus
. Thus
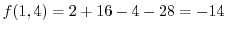 is the local minimum.
is the local minimum.
Since
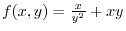 , we have
, we have
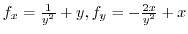 .
If
.
If 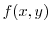 attains the extreme at
attains the extreme at
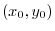 , then
, then
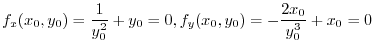
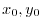 .Then
.Then
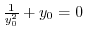 implies
implies
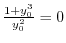 .Thus,
.Thus,
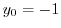 .Also,
.Also,
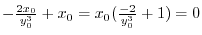 implies
implies 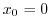 .
.
Next,
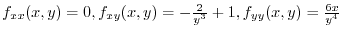 .
At
.
At 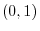 ,
,
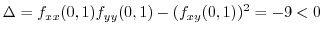
Since
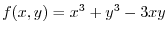 ,
,
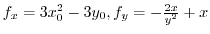 .
If
.
If 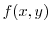 attains the extremum at
attains the extremum at
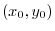 , then
, then
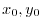 . Put
. Put
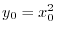 . Then
. Then
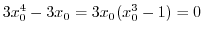
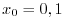 .Therefore,
.Therefore,
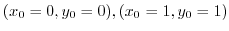 .
Next
.
Next
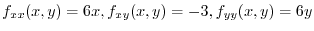 .
At
.
At 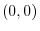 .
.
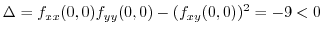
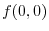 is not extremum.
At
is not extremum.
At 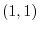 , we have
, we have
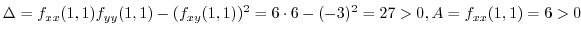
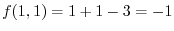 is the local minimum.
is the local minimum.
Since
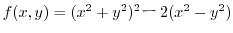 , we have
, we have
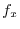 |
 |
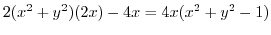 |
|
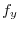 |
 |
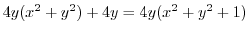 |
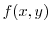 attains the extremum at
attains the extremum at
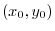 , then
, then
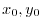 .Then
.Then
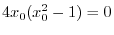
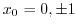 .Therefore,
.Therefore,
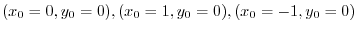 .
次に
.
次に
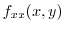 |
 |
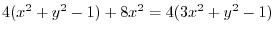 |
|
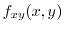 |
 |
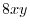 |
|
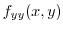 |
 |
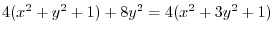 |
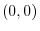 , we have
, we have
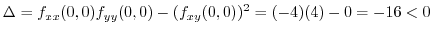
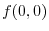 is not extremum.
is not extremum.
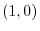 では
では
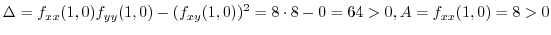
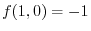 is local minimum.
At
is local minimum.
At 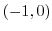 , we have
, we have
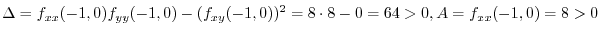
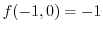 is th elocal minimum.
is th elocal minimum.
2.
By the Taylor's theorem, we have
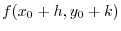 |
 |
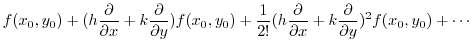 |
(a)
By the Taylor's theorem, let
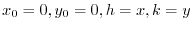 . Then
. Then
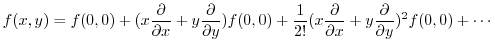
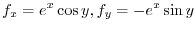
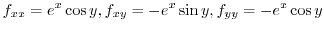
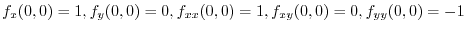
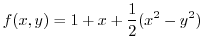
(b)
By the Taylor's theorem, we let
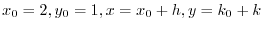 . Then
. Then
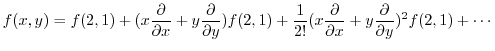
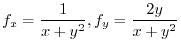
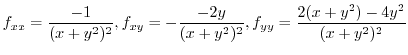
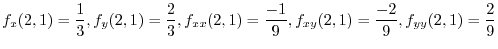
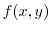 |
 |
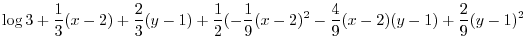 |