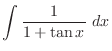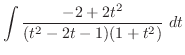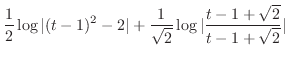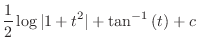3.5
1.
(a)
(b)
(c)
(d) Note that
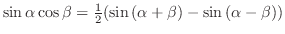 .
.
(e)
(f)
(g)
(h)
Thus 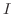 is given by
is given by
(i)
Alternate solution
(j)
Thus 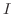 is given by
is given by
Thus, we need to find
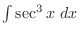 .
.
Thus,
Therefore,
(k) Let
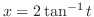 . Then
. Then
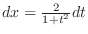 ,
,
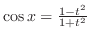 ,
,
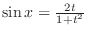 . Thus any trigonometric function can be written using rational functions.
. Thus any trigonometric function can be written using rational functions.
(l) Let
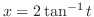 . Then
. Then
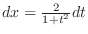 ,
,
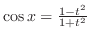 ,
,
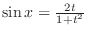
Now using partial fraction expansion on
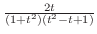 .
.
Clear the denominator. Then
Now matching the degee. Then we have
Then we have 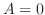 which implies that
which implies that
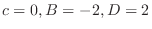 .Therefore,
.Therefore,
First we find
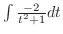 .
.
Next we find
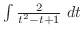 .
.
Now substitute
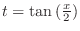 . Then
. Then
(m) Let
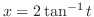 . Then
. Then
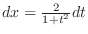 ,
,
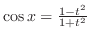 ,
,
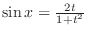 .
.
(n) You might set
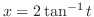 . But the all terms are square. So we let
. But the all terms are square. So we let
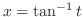 . Then
. Then
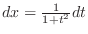 ,
,
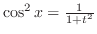 ,
,
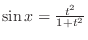 .
.
Now we use the partial fraction expansion..
Clear the denominator.
Here, we set
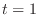 . Then
. Then
Set 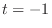 . Then
. Then
Now compare the coefficients of 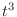 , we have
, we have 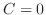 .
Finally, we compare the coefficients of
.
Finally, we compare the coefficients of 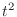 . Then
. Then
Thus,
Note that
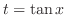 . Then
. Then
(o) Let
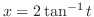 . Then
. Then
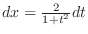 ,
,
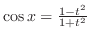 ,
,
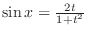 .
.
Using the partial fraction expansion, we have.
Clear the denominator.
Now we use the coefficient matching.
Coefficieints of 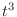
Coefficients of 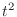
Coefficients of 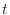
Constant term
Then we have
Thus,,
Now let 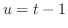 . Then
. Then 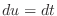 . Thus,
. Thus,
Then
Finally, substitute
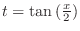 and we are done.
and we are done.
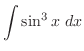

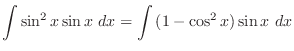

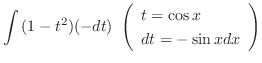

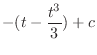

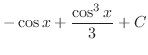
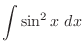

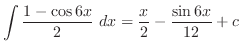
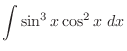

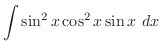

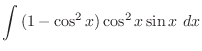

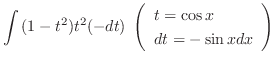

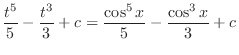
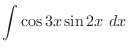

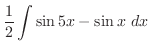

![$\displaystyle \frac{1}{2}[\frac{-\cos{5x}}{5} + \cos{x}] + c$](img905.png)
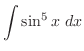

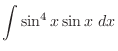

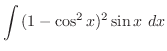

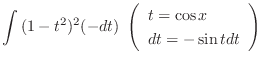

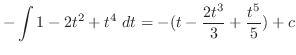

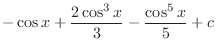
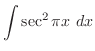

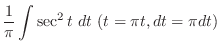

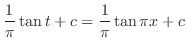
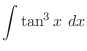

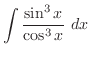

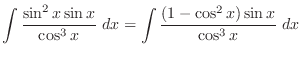

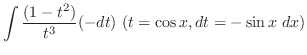

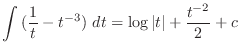

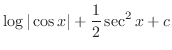

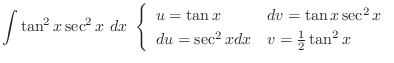

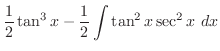

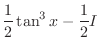
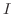 is given by
is given by
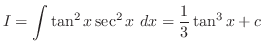
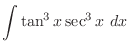

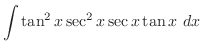

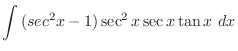

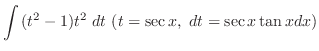

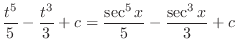
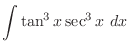

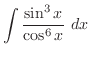

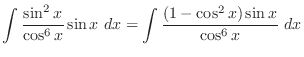

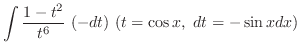

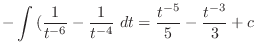

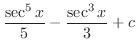

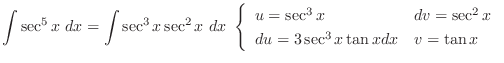

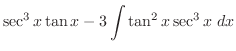

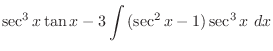

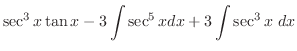

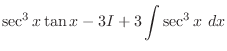
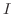 is given by
is given by
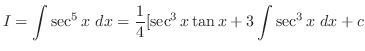
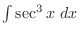 .
.

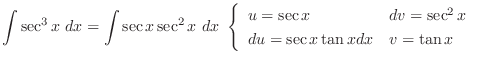

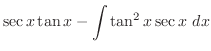

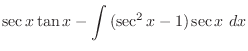

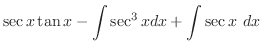

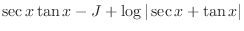
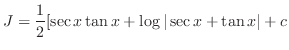
![$\displaystyle I = \frac{1}{4}[\sec^{3}{x}\tan{x} + \frac{3}{2}(\sec{x}\tan{x} + \log\vert sec{x} + \tan{x}] + c$](img949.png)
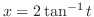 . Then
. Then
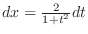 ,
,
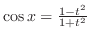 ,
,
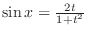 . Thus any trigonometric function can be written using rational functions.
. Thus any trigonometric function can be written using rational functions.
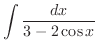

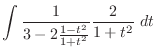

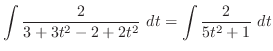

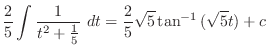

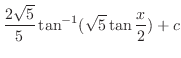
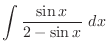

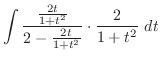

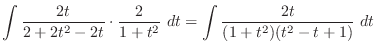
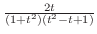 .
.
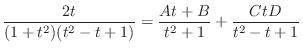
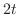

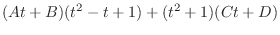

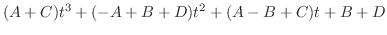
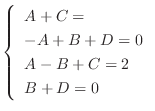
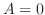 which implies that
which implies that
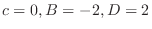 .Therefore,
.Therefore,
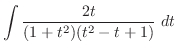

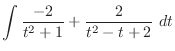
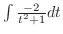 .
.
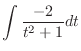

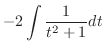

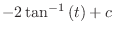
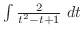 .
.
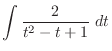

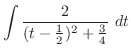

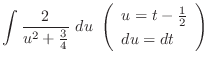

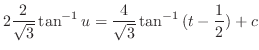
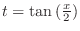 . Then
. Then
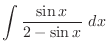

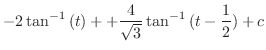

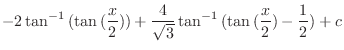

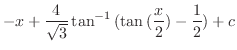
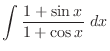

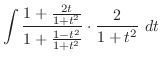

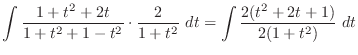

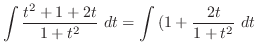

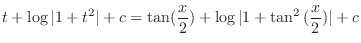
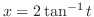 . But the all terms are square. So we let
. But the all terms are square. So we let
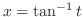 . Then
. Then
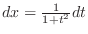 ,
,
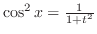 ,
,
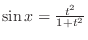 .
.
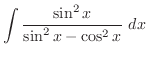

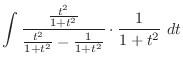

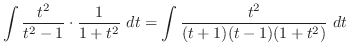
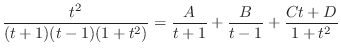
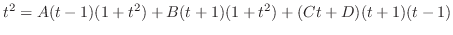
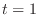 . Then
. Then
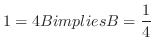
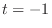 . Then
. Then
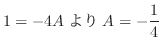
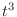 , we have
, we have 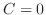 .
Finally, we compare the coefficients of
.
Finally, we compare the coefficients of 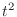 . Then
. Then
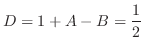
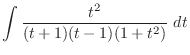

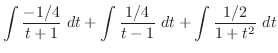

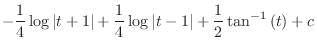
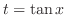 . Then
. Then
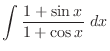

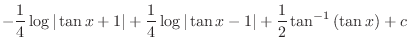

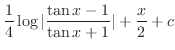
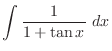

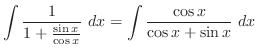

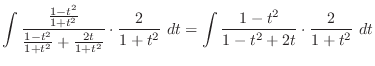

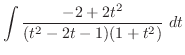
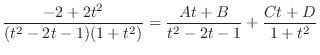
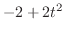

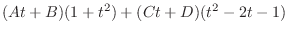

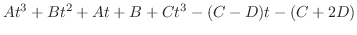
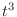
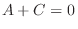
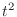
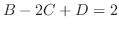
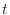
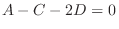
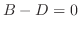
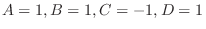
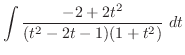

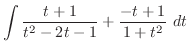

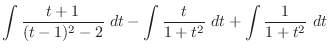
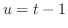 . Then
. Then 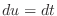 . Thus,
. Thus,
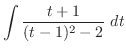

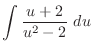

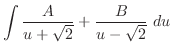

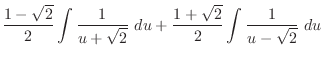

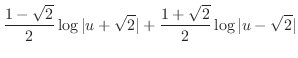

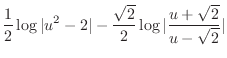

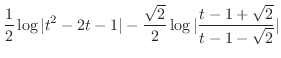
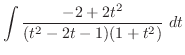

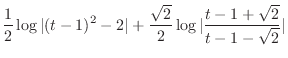
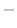
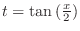 and we are done.
and we are done.