Next: Integration of trigonometric functions Up: INTEGRATION Previous: Iintegration of rational functions
3.4
1.
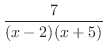 is rational function and the degree of the numerator
is rational function and the degree of the numerator 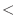 the degree of the denominator. So, we use the partial fraction expansion. Then
the degree of the denominator. So, we use the partial fraction expansion. Then
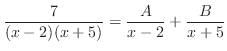
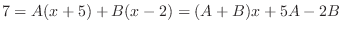
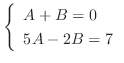
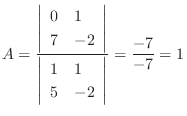
Putting these back into the equation above, we have 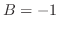 . Then
. Then
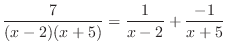
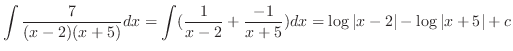
(b)
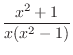 is a rational function with the degree of the numerato
is a rational function with the degree of the numerato  the degree of the denominator. Then using the partial fraction expansion, we have
the degree of the denominator. Then using the partial fraction expansion, we have
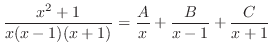
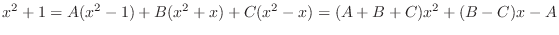
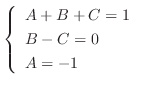
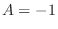 implies that
implies that
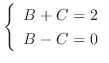
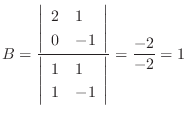
Put these back into the above equation. Then we have 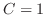 . Thus,
. Thus,
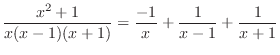
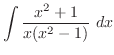 |
 |
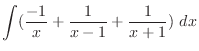 |
|
 |
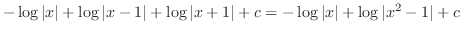 |
(c)
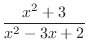 is a rational function with the degree of the numerator is greater than the degree of the denominator. So, divide the numerator by the denominator. Then
is a rational function with the degree of the numerator is greater than the degree of the denominator. So, divide the numerator by the denominator. Then
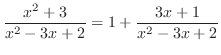
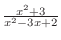 as
as
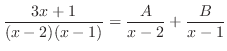
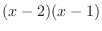 to both sides. Then
to both sides. Then
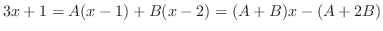
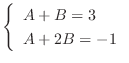
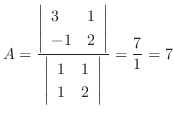
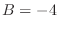 . Then
. Then
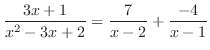
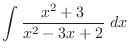 |
 |
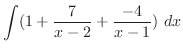 |
|
 |
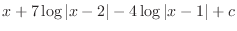 |
(d)
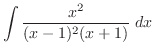 is a rational function with the degree of the numerator is less than the degree of the denominator. So, using the partial fraction expansion, we have
is a rational function with the degree of the numerator is less than the degree of the denominator. So, using the partial fraction expansion, we have
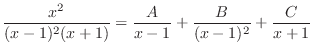
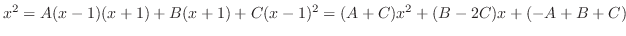
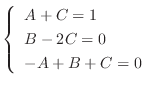
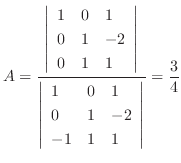
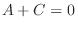 . Then
. Then
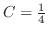 .Furthermore,
.Furthermore,
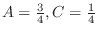 implies
implies
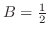 .Thus,
.Thus,
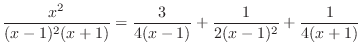
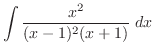 |
 |
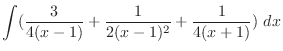 |
|
 |
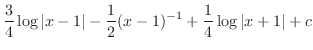 |
(e)
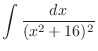 is a rational function with the degree of the numerator is less than the degree of the denominator. So, we might use the partial fraction expansion. But the numerator is already constant. It means that no more partial fraction expansion is necessary. In fact,
is a rational function with the degree of the numerator is less than the degree of the denominator. So, we might use the partial fraction expansion. But the numerator is already constant. It means that no more partial fraction expansion is necessary. In fact,
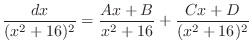
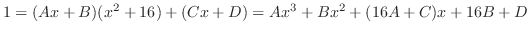
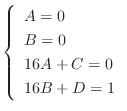
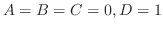 which is the original problem.
which is the original problem.
So, let
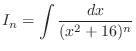 and use the integration by parts.
and use the integration by parts.
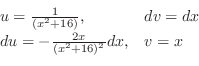
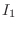 |
 |
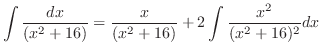 |
|
 |
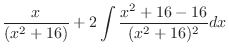 |
||
 |
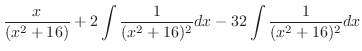 |
||
 |
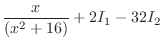 |
![$\displaystyle I_{2} = \frac{1}{32}[\frac{x}{(x^2 + 16)} + I_{1}] = \frac{1}{128}[\frac{4x}{(x^2 + 16)} + \tan^{-1}(\frac{x}{4})] + c$](img836.png)
Alternate solution (trig integral) Let
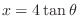 . Then
. Then
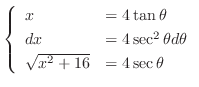
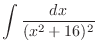 |
 |
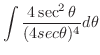 |
|
 |
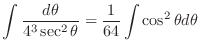 |
||
 |
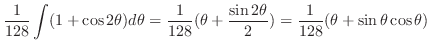 |
||
 |
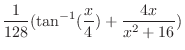 |
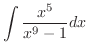 |
 |
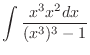 |
|
 |
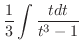 |
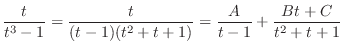
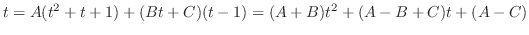
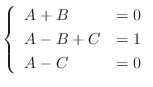
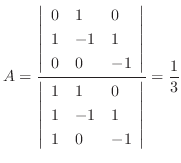
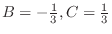 and
and
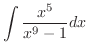 |
 |
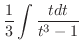 |
|
 |
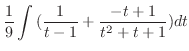 |
||
 |
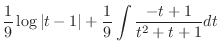 |
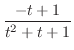 as follows:
as follows:
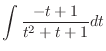 |
 |
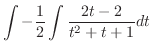 |
|
 |
![$\displaystyle -\frac{1}{2}\int{\frac{2t + 1 -3 }{t^2 + t+1}}dt = -\frac{1}{2}[\...
...ac{2t + 1}{t^2 + t+1}}dt + \int\frac{-3 }{(t + \frac{1}{2})^2 + \frac{3}{4}}dt]$](img859.png) |
||
 |
![$\displaystyle -\frac{1}{2}[\log\vert t^2 + t+1\vert -3 \frac{2}{\sqrt{3}}\tan^{-1}{(\frac{2(t+\frac{1}{2})}{\sqrt{3}})}]$](img860.png) |
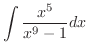 |
 |
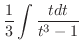 |
|
 |
![$\displaystyle \frac{1}{9}\log\vert t-1\vert + \frac{1}{9}(-\frac{1}{2})[\log\ve...
...t+1\vert -3 \frac{2}{\sqrt{3}}\tan^{-1}{(\frac{2(t+\frac{1}{2})}{\sqrt{3}})}]+c$](img861.png) |
||
 |
![$\displaystyle \frac{1}{9}\log\vert x^3 -1\vert - \frac{1}{18}[\log\vert x^6 + x^3 + 1\vert + 2\sqrt{3} \tan^{-1}{(\frac{2x^3+1}{\sqrt{3}})}]+c$](img862.png) |
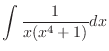 |
 |
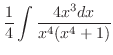 |
|
 |
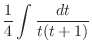 |
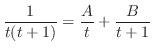
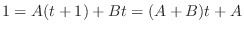
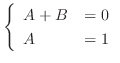
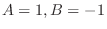 .
.
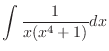 |
 |
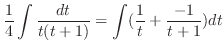 |
|
 |
![$\displaystyle \frac{1}{4}[\log\vert t\vert - \log\vert t+1\vert] + c$](img873.png) |
||
 |
![$\displaystyle \frac{1}{4}[\log\vert x^4\vert - \log\vert x^4+1\vert] + c$](img874.png) |