Next: Taylor's theorem Up: 微分法(DEFFERENTIATION) Previous: Limit of indeterminate forms
2.7
1.
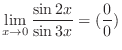 which is indeterminate form. Then by L'Hospital's rule, we have
which is indeterminate form. Then by L'Hospital's rule, we have
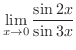 |
 |
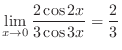 |
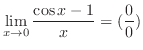 which is indeterminate form. Then by L'Hospital's rule,
which is indeterminate form. Then by L'Hospital's rule,
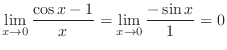
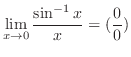 which is indeterminate form. Then by L'Hospital's rule,
which is indeterminate form. Then by L'Hospital's rule,
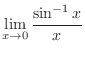 |
 |
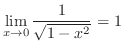 |
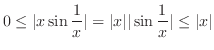
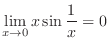
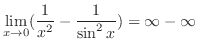 which is indeterminate form.To use L'Hospital's rule, it must be of the indeterminate form
which is indeterminate form.To use L'Hospital's rule, it must be of the indeterminate form
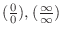 . So, rewrite
. So, rewrite
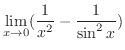 |
 |
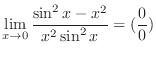 |
|
 |
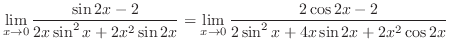 |
||
 |
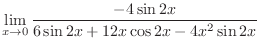 |
||
 |
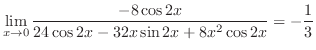 |
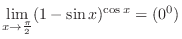 which is indeterminate form. To use L'Hospital's rule, it must be of the indeterminate form
which is indeterminate form. To use L'Hospital's rule, it must be of the indeterminate form
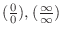 .Note that
.Note that
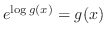 . Then
. Then
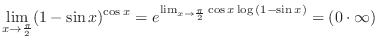 .もう一度変形すると
.もう一度変形すると
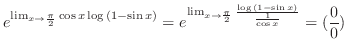 よって
よって
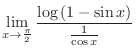 にL'Hospitalの定理を用いると
にL'Hospitalの定理を用いると
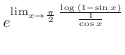 |
 |
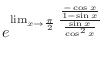 |
|
 |
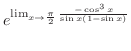 |
||
 |
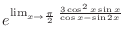 |
||
 |
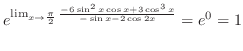 |
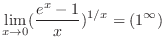 which is indeterminate form. To use L'Hospital's rule, it must be of the indeterminate form
which is indeterminate form. To use L'Hospital's rule, it must be of the indeterminate form
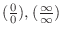 . Note that
. Note that
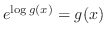 . Then
. Then
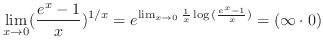 which is indeterminate form.So, we rewrite
which is indeterminate form.So, we rewrite
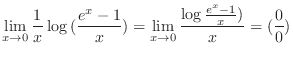 which is indeterminate form. Then by L'Hospital's rule, we have
which is indeterminate form. Then by L'Hospital's rule, we have
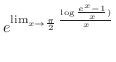 |
 |
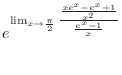 |
|
 |
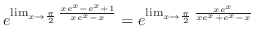 |
||
 |
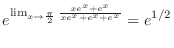 |
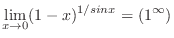 which is indeterminate form. To use L'Hospital's rule, it must be of the indeterminate form
which is indeterminate form. To use L'Hospital's rule, it must be of the indeterminate form
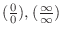 .Note that
.Note that
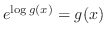 .
.
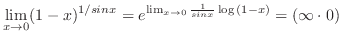 which is indeterminate form.So, rewrite
which is indeterminate form.So, rewrite
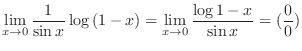 which is indeterminate form.
Thus by L'Hospital's rule, we have
which is indeterminate form.
Thus by L'Hospital's rule, we have
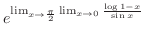 |
 |
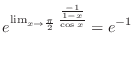 |