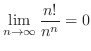Next: Definition of transcendental functions Up: FUNCTIONS Previous: Euler e
1.7
1.
(a)For any number 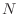 is chosen, there is a number
is chosen, there is a number 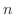 so that
so that
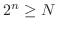 . Thus, it is unbounded.
. Thus, it is unbounded.
(b)
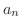 represents
represents 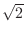 to the
to the 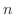 th decimal place. So even as
th decimal place. So even as 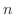 gets larger, it can not be greater than
gets larger, it can not be greater than 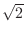 . Thus it is bounded.
. Thus it is bounded.
2.
(a)Let
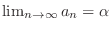 . Then
. Then
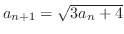 . Thus
. Thus
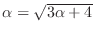 . Now square both sides, we have
. Now square both sides, we have
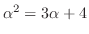 . Thus,
. Thus,
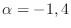 . By the initial condition
. By the initial condition 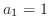 , then
, then
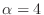 .We next show that
.We next show that
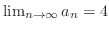 . By the theorem1.13, we need to show that the exists
. By the theorem1.13, we need to show that the exists
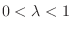 so that
so that
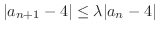 .
.
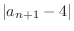 |
 |
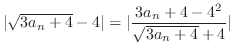 |
|
 |
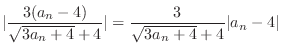 |
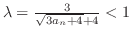
3.
![$\displaystyle \lim_{n \to \infty}(1 + \frac{2}{n})^{n} = \lim_{m \to \infty}[(1 + \frac{1}{m})^{m}]^{2} = e^{2} $](img322.png)
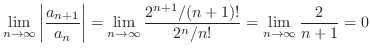
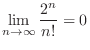
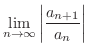 |
 |
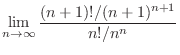 |
|
 |
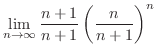 |
||
 |
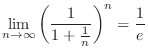 |