Next: Probabilistic model Up: Sample Space Previous: Sample Space Contents
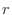 objects from different
objects from different 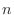 objects is
objects is
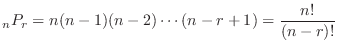
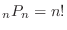 ,
,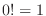 .
.
 objects from
objects from  objects with repetetion is
objects with repetetion is
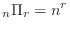
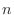 pieces in a circle is
pieces in a circle is
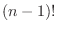
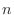 objects with
objects with 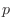 identical objects of type 1,
identical objects of type 1, 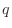 identical objects of type 2,
identical objects of type 2, 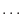 ?and
?and 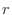 identical objects of type k is
identical objects of type k is
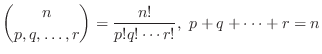
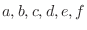 in the following sequence.
in the following sequence.
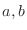 are next to each other
are next to each other
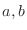 are not next to each other
are not next to each other
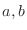 are place to the each end
are place to the each end
5. Show that the number of outcomes when arranging
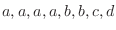 in a sequence is given by
in a sequence is given by
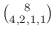 .
.
1
(a) Consider the number of outcomes by putting the integers in
 . First of all, it has to be 4-digit integer. Thus we can not use 0 in the thousands. Then we have a choice of one of integers. Thus, there are 6 outcomes. For hundreds through ones, we can use any of the integers. But we can not use the same integer twice.
Then there are 6 outcomes in the hundreds, 5 outcomes in the tens, 4 outcomes in the ones. Thus, total of
. First of all, it has to be 4-digit integer. Thus we can not use 0 in the thousands. Then we have a choice of one of integers. Thus, there are 6 outcomes. For hundreds through ones, we can use any of the integers. But we can not use the same integer twice.
Then there are 6 outcomes in the hundreds, 5 outcomes in the tens, 4 outcomes in the ones. Thus, total of
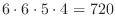
(b) Note that multiples of 5 always have a ones digit of 0 or 5.Next, note that the case where the ones digit is 0 and the case where it is 5 are considered separately
When the ones place is 0.
Thousands, hundreds, and tens can use numbers from 1 to 6 once. The number of permutations to take out 3 out of 6 is
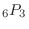 .Therefore, 120
.Therefore, 120
When the ones place is 5.
We can not use 0 in the thousands. Thus, there are 5 outcomes in the thousands. There are 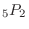 outcomes for the hundreds and tens and
outcomes for the hundreds and tens and
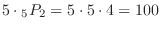 outcomes in the ones. Thus,
outcomes in the ones. Thus,
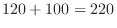
(c) Here we can use the same number. Now the are 6 outcomes in the thousands and 7 outcomes in the hunreds, tens, and ones.,Therefore,
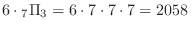
2
(a)
The number of outcomes for taking 6 cards from 10 different cards is
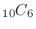 . Now
. Now
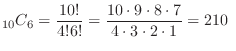
(b)
Cards 1 and 2 have to be in the arrangement. So, we consider the number of outcomes of selecting 4 cards from 8 cards. Thus we have
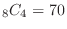 .
.
(c) Let 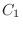 be the case where 1 is included and
be the case where 1 is included and 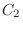 be the case where 2 is included. Then there are
be the case where 2 is included. Then there are
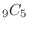 outcomes in
outcomes in 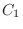 and
and
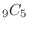 outcomes in
outcomes in 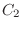 . Thus, the outcomes for which the card 1 or 2 is included is
. Thus, the outcomes for which the card 1 or 2 is included is
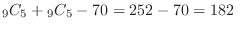
3
(a)
 number of heads is i
number of heads is i![$]$](img33.png) .Then the heads can be shown
.Then the heads can be shown 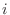 times whithin 5 trials. Thus, the number of outcomes is
times whithin 5 trials. Thus, the number of outcomes is
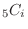 .
.
The number of outcomes of 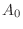 is
is
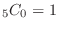 ,
,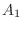 is
is
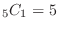 ,
,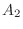 is
is
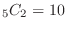 ,
,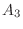 is
is
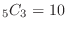 ,
, 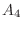 is
is
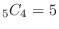 ,
,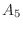 is
is
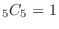
(b) In all possible cases, the number of outcomes is
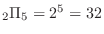 .
.
4
(a) Since 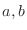 are nect to each other,let
are nect to each other,let 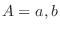 . Then we have
. Then we have 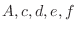 .Thus, the nuber of outcomes is
.Thus, the nuber of outcomes is
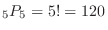
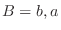 . Then the number of outcomes is
. Then the number of outcomes is
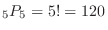
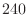 .
.
(b) Let 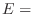 [
[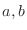 are not next to each other]. Then
are not next to each other]. Then 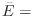 [
[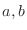 are next to each other]. Thus the number of outcomes of
are next to each other]. Thus the number of outcomes of 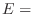
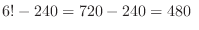
(c) 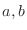 are at the ends. Then there are two cases.
case 1.
are at the ends. Then there are two cases.
case 1.
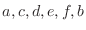 . Then the number of arrangements of
. Then the number of arrangements of 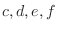 is
is
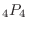 case 2.
case 2.
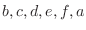 . Then the number of arrangements of
. Then the number of arrangements of 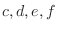 is
is
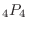 .
Thus,
.
Thus,
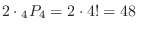
5
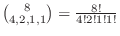 .If you number all and arrange them, then the number of outcomes is
.If you number all and arrange them, then the number of outcomes is
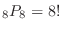 .But there are 4
.But there are 4 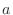 's. 2
's. 2 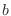 's. They can not be distinguished. So, the number of outcomes is
's. They can not be distinguished. So, the number of outcomes is
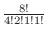 .
.