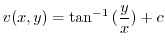Next: 4.4 Cauchy's integral formula Up: Solution Previous: 4.2 Complex integral Index
1.
Let  be the curve connecting from a starting point
be the curve connecting from a starting point  to
to  . Then the curve connecting from a point
. Then the curve connecting from a point 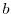 to
to 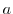 can be represented by
can be represented by 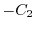 . Now let
. Now let
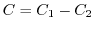 . Then the curve
. Then the curve 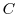 is a closed curve in the region
is a closed curve in the region  . Here using Cauchy's integral theorem, we have
. Here using Cauchy's integral theorem, we have
| 0 |  |
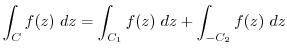 |
|
 |
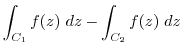 |
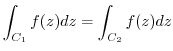
First, bridge from curve 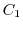 to curve
to curve 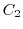 . Then, while turning along the curve
. Then, while turning along the curve 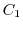 , cross the bridge and move to the curve
, cross the bridge and move to the curve 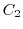 , Let
, Let 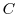 be the curve that goes in the opposite direction, crosses the original bridge, returns to the curve
be the curve that goes in the opposite direction, crosses the original bridge, returns to the curve 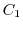 , and goes around.
At this time,
, and goes around.
At this time, 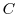 is a closed curve included in the region
is a closed curve included in the region  , so if Cauchy's integral theorem is used,
, so if Cauchy's integral theorem is used,
| 0 |  |
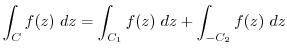 |
|
 |
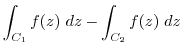 |
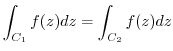
Since the curve  is the circumference of a radius
is the circumference of a radius 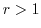 centered at the origin,
centered at the origin,
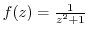 is not analytic inside of this circle. Then, expand
is not analytic inside of this circle. Then, expand
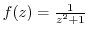 by using partial fraction.
by using partial fraction.
![$\displaystyle \frac{1}{z^2 + 1} = \frac{1}{(z+i)(z-i)} = \frac{1}{2i}[\frac{1}{z-i} - \frac{1}{z+i}]$](img642.png)
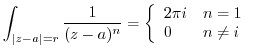
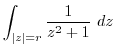 |
 |
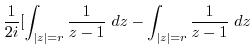 |
|
 |
![$\displaystyle \frac{1}{2i}[2\pi i - 2\pi i] = 0$](img646.png) |
Since the curve 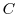 is the circumference of a radius
is the circumference of a radius 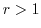 centered at the origin,
centered at the origin,
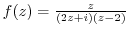 is not analytic inside of this circle. Then , expand
is not analytic inside of this circle. Then , expand
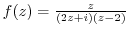 by using the partial fraction expansion.
by using the partial fraction expansion.
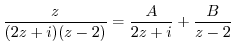
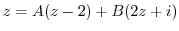
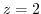 . Then
. Then
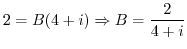
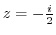 . Then
. Then
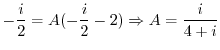
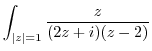 |
 |
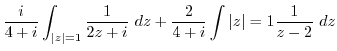 |
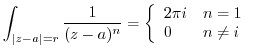
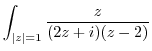 |
 |
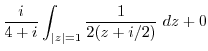 |
|
 |
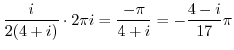 |
Since this curve is centered on the origin, the circumference of the upper half of a circle with radius r> 1, and the diameter on the real axis,
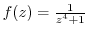 is not analytic inside of this circle. Then expand
is not analytic inside of this circle. Then expand
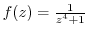 by using the partial fraction expansion.
Solutions of
by using the partial fraction expansion.
Solutions of 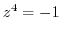 are give by
are give by
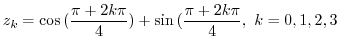
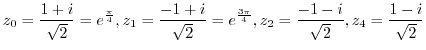
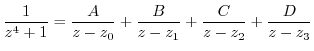
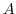 and
and 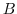 .
.
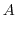 |
 |
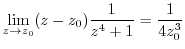 |
|
 |
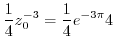 |
||
 |
 |
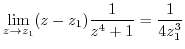 |
|
 |
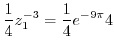 |
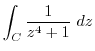 |
 |
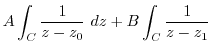 |
|
 |
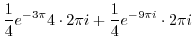 |
||
 |
![$\displaystyle \frac{\pi i}{2}[e^{\frac{-3\pi i}{4}} + e^{\frac{-9 \pi i}{4}}]$](img674.png) |
||
 |
![$\displaystyle \frac{\pi i}{2}[\frac{-1-i}{\sqrt{2}} + \frac{1-i}{\sqrt{2}}] = \frac{\pi}{2}$](img675.png) |
3.
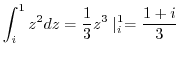
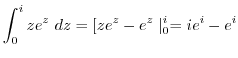
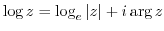
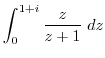 |
 |
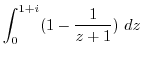 |
|
 |
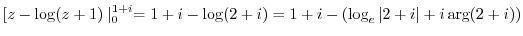 |
||
 |
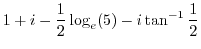 |
||
 |
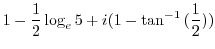 |
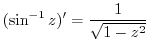
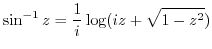
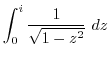 |
 |
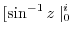 |
|
 |
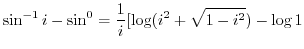 |
||
 |
![$\displaystyle \frac{1}{i}\log(-1 + \sqrt{2}) = \frac{1}{i}[\log_{e}\vert-1 + \sqrt{2}\vert + i\arg(-1 + \sqrt{2})]$](img689.png) |
||
 |
![$\displaystyle \frac{1}{i}[\log_{e}(\sqrt{2} - 1)]$](img690.png) |
4. A function 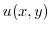 is called a harmonic function if
is called a harmonic function if
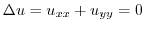 . Also,
. Also, 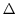 is said to be Laplacian, the equation
is said to be Laplacian, the equation
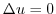 is called a Laplace equation. Make sure that the holomorphic function
is called a Laplace equation. Make sure that the holomorphic function
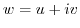 with
with 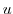 in the real part satisfies Cauchy-Riemann's equation.
in the real part satisfies Cauchy-Riemann's equation.
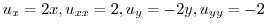
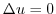 and
and 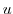 is a harmonic function. Next find a holomorphic function
is a harmonic function. Next find a holomorphic function 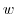 which has
which has 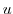 as a real part. Let
as a real part. Let
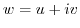 . Then
. Then
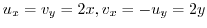
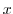 ,
Now by the condition
,
Now by the condition
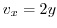 , we have
, we have
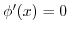 which implies
which implies
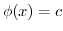 and
and
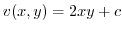
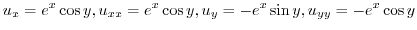
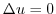 and
and  is a harmonic function. Next find
is a harmonic function. Next find 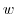 which has
which has 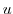 as a real part. Let
as a real part. Let
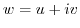 . Then
. Then
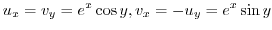
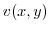 |
 |
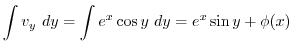 |
|
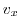 |
 |
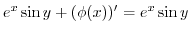 implies implies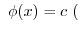 constant constant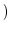 |
|
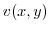 |
 |
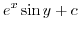 |
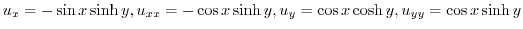
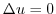 and
and  is a harmonic function. Next find
is a harmonic function. Next find  which has
which has 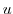 as a real part. Let
as a real part. Let
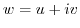 . Then
. Then
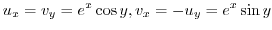
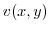 |
 |
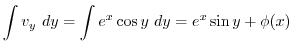 |
|
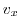 |
 |
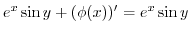 implies implies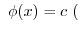 constant constant |
|
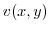 |
 |
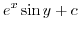 |
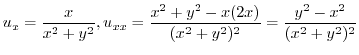
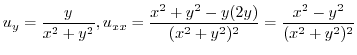
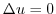 and
and 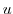 is a harmonic function. Next find
is a harmonic function. Next find 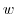 which has
which has 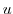 as a real part. Let
as a real part. Let
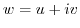 . Then
. Then
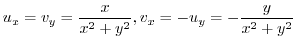
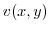 |
 |
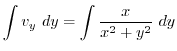 |
|
 |
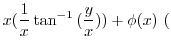 note note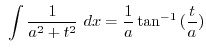 |
||
 |
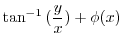 |
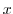 ,
,
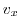 |
 |
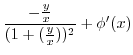 |
|
 |
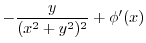 |
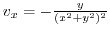 . Thus
. Thus
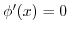 and
and
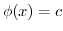 . Therefore,
. Therefore,