Next: 2.4 Inverse function of Up: Solution Previous: Linear function Index
1.
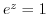 implies
implies
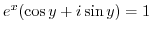 . Note that two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. Thus we obtain the following system of equations.
. Note that two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. Thus we obtain the following system of equations.
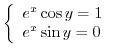
Note that
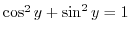 . Then
. Then
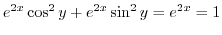
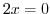 . That is
. That is 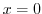 . Putting this into the above equation, we have
. Putting this into the above equation, we have
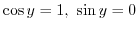 . Thus,
. Thus,
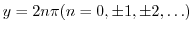 . Therefore,
. Therefore, 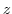 saitisfies
saitisfies
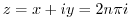
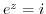 implies
implies
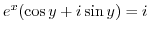 . Note that two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. Then we have the following system of equations.
. Note that two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. Then we have the following system of equations.
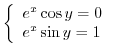
Note that
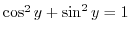 . Then
. Then
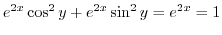
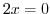 . That is
. That is 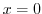 . Putting this into the above equation, we have
. Putting this into the above equation, we have
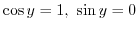 . Thus,
. Thus,
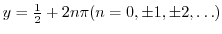 . Therefore
. Therefore 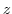 is
is
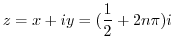
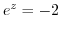 implies
implies
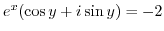 . Note that two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. Then we have the following system of equations.
. Note that two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. Then we have the following system of equations.
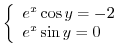
Note that
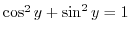 .
.
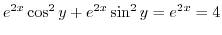
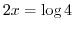 . That is
. That is
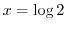 . Putting this into the above equation, we have
. Putting this into the above equation, we have
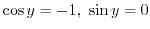 . Thus,
. Thus,
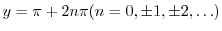 . Therefore,
. Therefore, 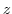 is
is
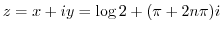
(a) Trigonometric functions are once rewritten using exponential functions. After that, the polar form can be changed to the orthogonal form.
When 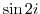 is expressed using an exponential function, we have
is expressed using an exponential function, we have
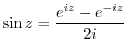
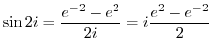
(b) Simplify using the addition theorem.
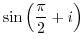 |
 |
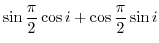 |
|
 |
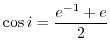 |
(c) Simplify using the addition theorem.
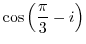 |
 |
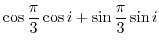 |
|
 |
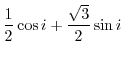 |
||
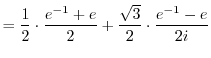 |
|||
 |
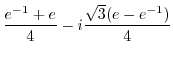 |
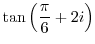 |
 |
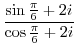 |
|
 |
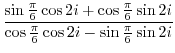 |
||
 |
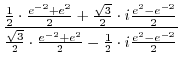 |
||
 |
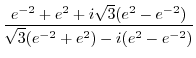 |
||
 |
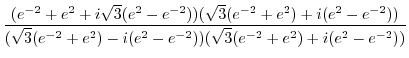 |
||
 |
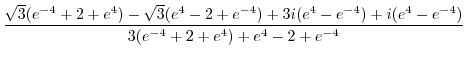 |
||
 |
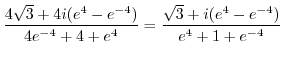 |
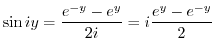
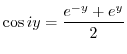
3.
Divide
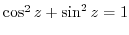 by
by
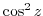 . Then
. Then
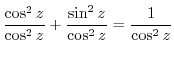
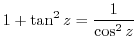
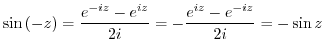
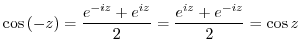
4.
(a) Of the 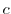 that satisfies
that satisfies
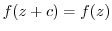 , the one with the smallest
, the one with the smallest 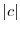 is called the period of the function
is called the period of the function 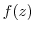 . Note also that
. Note also that
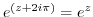 .
.
Let
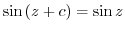 . Then find the value of
. Then find the value of 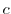 .
.
Since
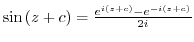 , let
, let
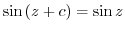 . Then
. Then
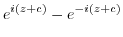 |
 |
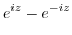 |
|
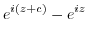 |
 |
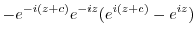 |
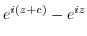 is the common term. Thus,
is the common term. Thus,
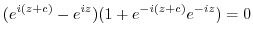
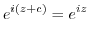 or
or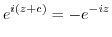
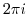 . Then
. Then
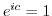 implies
implies 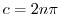 . Also,
. Also,
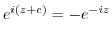 implies
implies
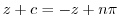 .
.
5.
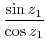 |
 |
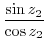 |
|
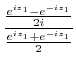 |
 |
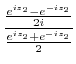 |
|
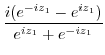 |
 |
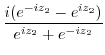 |
|
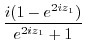 |
 |
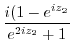 |
|
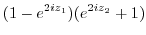 |
 |
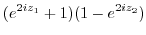 |
|
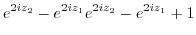 |
 |
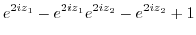 |
|
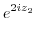 |
 |
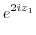 |
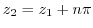 . Therefore,
. Therefore, 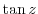 has the period
has the period 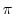 .
.