Exercise5.3
1.
Find the residue at the singularity of the following function (m is positive real number).
- (a)
-
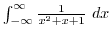
- (b)
-
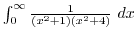
- (c)
-
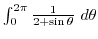
- (d)
-
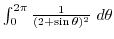
- (e)
-
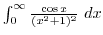
- (f)
-
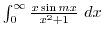
- (g)
-
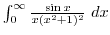
- (h)
-
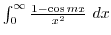
2. Find the following integral using complex integration (a is positive constant)
- (a)
-
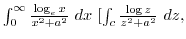 C is fig19.5
C is fig19.5
- (b)
-
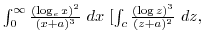 C is fig19.7
C is fig19.7
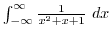
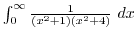
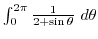
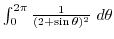
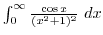
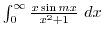
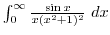
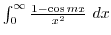
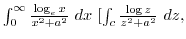 C is fig19.5
C is fig19.5
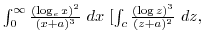 C is fig19.7
C is fig19.7