Line integral and Green's theorem

Exercise4.1

1. Find the following line integrals.

(a)

$\int_{c}y dx, C: y = 1 -x, 0 \leq x \leq 1$

(b)

$\int_{c}x^2 dy, C: y = 1 -x, 0 \leq x \leq 1$

(c)

$\int_{c}(xy dx - y^2 dy), C: y = x^2, -1 \leq x \leq 1$

(d)

$\int_{c}(xy dx - x^3 dy), C: x = \cos{\theta}, y = \sin{\theta}, 0 \leq \theta \leq 2\pi$

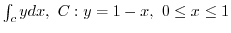
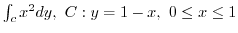
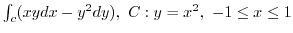
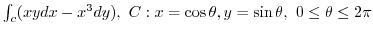
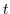
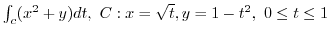
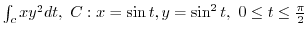
2. Find the following line integral for the parameter $t$

(a)

$\int_{c}(x^2 + y)dt, C: x = \sqrt{t}, y = 1 - t^2, 0 \leq t \leq 1$

(b)

$\int_{c}xy^2 dt, C: x = \sin{t}, y = \sin^{2}{t}, 0 \leq t \leq \frac{\pi}{2}$

3. Using Green's theorem, evaluate the following line integral.

(a)

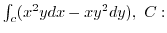$\int_{c}(x^2 y dx - xy^2 dy), C:$   unit circle

(b)

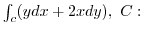$\int_{c}(y dx + 2x dy), C:$   first quadrand quater circle