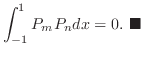Next: 演習問題6.4 Up: フーリエ級数(Fourier series) Previous: 演習問題6.3 目次 索引
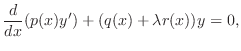
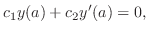
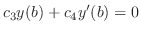
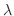 は実数をとり,自明でない解が存在するとき
は実数をとり,自明でない解が存在するとき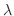 を固有値(eigenvalue)といい,自明でない解を固有関数(eigenfunction)といいます.
を固有値(eigenvalue)といい,自明でない解を固有関数(eigenfunction)といいます.
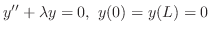 の固有値は
の固有値は
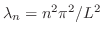 で固有関数は
で固有関数は
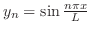 で与えられることを示せ.
で与えられることを示せ.
解
(1)
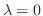 のとき,
のとき,
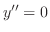 より
より
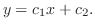
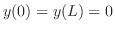 を用いると
を用いると
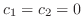 となり,
となり,
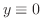 .
.
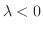 のとき,
のとき,
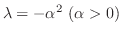 とおくと
とおくと
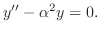
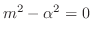 より,
より,
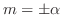 .よって
.よって
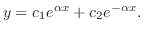
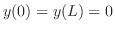 を用いると
を用いると
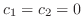 となり,
となり,
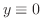 .
.
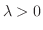 のとき,
のとき,
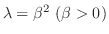 とおくと
とおくと
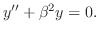
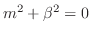 より,
より,
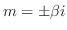 .よって
.よって
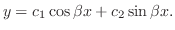
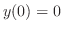 より
より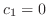 .つぎに
.つぎに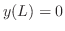 より
より
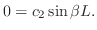
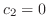 ならば自明でない解が存在しない.そこで自明でない解が存在するためには,
ならば自明でない解が存在しない.そこで自明でない解が存在するためには,
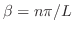 .よって固有値は
.よって固有値は
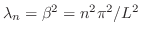 ,固有関数は
,固有関数は
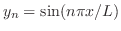 となる.
となる.

![$\displaystyle \frac{d}{dx}[(1-x^{2})y^{\prime}] + \lambda y = 0. $](img1904.png)
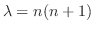 ,ただし
,ただし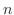 が負でない整数のとき,この微分方程式は多項式の解をもちます.この解を
が負でない整数のとき,この微分方程式は多項式の解をもちます.この解を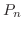 で表わし,位数
で表わし,位数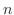 のLegendreの多項式といいます.最初のいくつかのLegendreの多項式を表わすと次のようになります.
のLegendreの多項式といいます.最初のいくつかのLegendreの多項式を表わすと次のようになります.
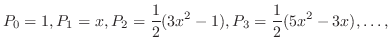
![$[-1,1]$](img1908.png) で直交系をなすことを示せ.
で直交系をなすことを示せ.
解
Legendreの多項式
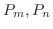 は固有値
は固有値
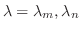 に対する固有関数である.よって
に対する固有関数である.よって
![$\displaystyle \frac{d}{dx}[(1-x^{2}) P_{m}^{\prime}] + \lambda_{m} P_{m} = 0, $](img1911.png)
![$\displaystyle \frac{d}{dx}[(1-x^{2}) P_{n}^{\prime}] + \lambda_{m} P_{n} = 0. $](img1912.png)
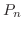 を次の式に
を次の式に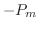 を掛けて加えると,
を掛けて加えると,
![$\displaystyle (\lambda_{m} - \lambda_{n})P_{m}P_{n} = \frac{d}{dx}[(1-x^{2})P_{...
...t_{}^{x} P_{m}dt] - \frac{d}{dx}[(1-x^{2})P_{m}^{\prime}\int_{}^{x} P_{n}dt] . $](img1914.png)
![$[-1,1]$](img1908.png) で積分すると
で積分すると
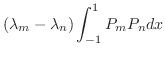 |
 |
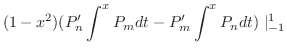 |
|
 |
 |
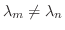 のとき
のとき