Next: 演習問題6.1 Up: フーリエ級数(Fourier series) Previous: フーリエ級数(Fourier series) 目次 索引
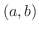 で区分的に連続な関数(piecewise continuous function)の集まりからなる
で区分的に連続な関数(piecewise continuous function)の集まりからなる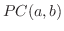 について考えます.
について考えます.
幾何ベクトルについて次の3つのことはよく知っていると思います.(1)和,(2)スカラー倍,(3)内積(スカラー積).これまでに私たちは和およびスカラー倍の一般化を行いました.そこでここでは内積の一般化に挑戦します.
|
定義 6..1
2つのベクトル
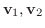 に対して,実数 に対して,実数
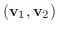 が定まり,次の性質をもつとき, が定まり,次の性質をもつとき,
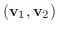 または または
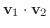 を を
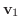 と と
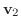 の内積(inner product)という. の内積(inner product)という.
あるベクトル空間のすべてのベクトル
|
|
定義 6..2
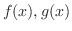 を を![$PC[a,b]$](img1695.png) の元とすると,内積 の元とすると,内積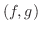 は次の式で与えられる. は次の式で与えられる.
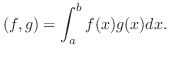
(注) これは内積の性質
|
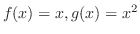 が
が![$PC[0,2]$](img1699.png) に属しているとき,内積
に属しているとき,内積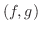 を計算せよ.
を計算せよ.
解
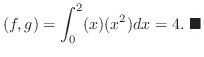
ベクトル空間上に内積が定義されると,ノルム(ベクトルの大きさ)が定義されます.
|
定義 6..3
ベクトルvのノルム(norm)は
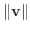 で表わされ,次の式で与えられる. で表わされ,次の式で与えられる.
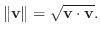
|
幾何ベクトル空間では,
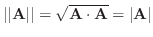 となるのでAの長さと同じです.三次元ベクトル空間では
となるのでAの長さと同じです.三次元ベクトル空間では
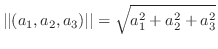
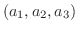 までの距離と考えられます.関数空間(function space)
までの距離と考えられます.関数空間(function space)![$PC[a,b]$](img1695.png) では,
では,
![$\displaystyle \vert\vert f\vert\vert = \{\int_{a}^{b}[f(x)]^2dx\}^{1/2} . $](img1706.png)
ベクトル空間に内積が定義されると,ノルムだけでなく垂直という概念の一般化として直交を定義できます.
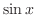 と
と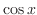 は
は
![$[-\pi,\pi]$](img1710.png) で直交するが
で直交するが![$[0,\pi/4]$](img1711.png) では直交しないことを示せ.
では直交しないことを示せ.
解
[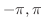 ]で
]で
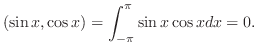
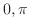 ]で
]で
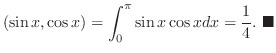
関数空間での直交は直角に交わるということではありません.注意して下さい.
0でない幾何ベクトルAをその大きさで割り単位ベクトル
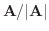 を求めることがよくあります.もっと一般的な場合にも,ベクトルvをそのノルムで割り,単位ベクトル
を求めることがよくあります.もっと一般的な場合にも,ベクトルvをそのノルムで割り,単位ベクトル
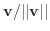 を作ります.このようにして大きさが1のベクトルを作ることを,正規化(normalize)するといいます.また直交系のすべてのベクトルを正規化してできた集合を正規直交系(orthonormal system)といいます.正規直交系の例として三次元ベクトル空間での{i,j,k}があげられます.
を作ります.このようにして大きさが1のベクトルを作ることを,正規化(normalize)するといいます.また直交系のすべてのベクトルを正規化してできた集合を正規直交系(orthonormal system)といいます.正規直交系の例として三次元ベクトル空間での{i,j,k}があげられます.
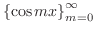 は
は![$[0,\pi]$](img1719.png) で直交系をなすことを示し,対応する正規直交系を求めよ.
で直交系をなすことを示し,対応する正規直交系を求めよ.
解
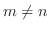 のとき,
のとき,
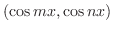 |
 |
 |
|
 |
![$\displaystyle \frac{1}{2}\int_{0}^{\pi}[\cos{(m+n)x} + \cos{(m-n)x}]dx$](img1723.png) |
||
 |
![$\displaystyle [\frac{\sin{(m+n)x}}{2(m+n)} + \frac{\sin{(m-n)x}}{2(m-n)}] \mid_{0}^{\pi} = 0 .$](img1724.png) |
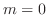 のとき,
のとき,
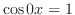 で
で
![$\displaystyle \vert\vert 1 \vert\vert = [ \int_{0}^{\pi}(1)^2 dx]^{1/2} = \sqrt{\pi}. $](img1727.png)
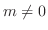 のとき,
のとき,
![$\displaystyle \vert\vert\cos{mx}\vert\vert = [ \int_{0}^{\pi}\cos^2{mx} dx]^{1/2} = \sqrt{\pi/2}. $](img1729.png)
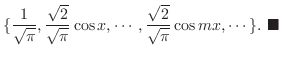
ノルムはベクトル空間上の任意のベクトル
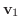 と
と
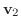 に対して,三角不等式
に対して,三角不等式
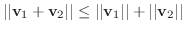
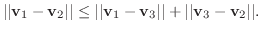
![$PC[0,2]$](img1699.png) において,
において, と
と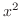 の距離を求めよ.
の距離を求めよ.
解
![$\displaystyle \vert\vert x - x^2\vert\vert = [\int_{0}^{2}(x -x^2)^2 dx]^{1/2} = \frac{4}{\sqrt{15}} .
\ensuremath{ \blacksquare}
$](img1734.png)