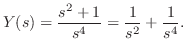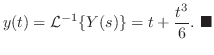Next: 演習問題5.6 Up: ラプラス変換(The Laplace transformation) Previous: 演習問題5.5 目次 索引
|
定義 5..5
関数
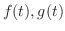 は区分的に連続な関数であるとする.そのとき合成積 は区分的に連続な関数であるとする.そのとき合成積
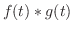 は次のように定義される. は次のように定義される.
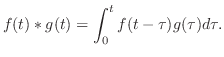
|
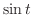 と
と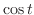 の合成積を求めよ.
の合成積を求めよ.
解
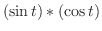 |
 |
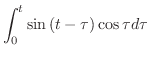 |
|
 |
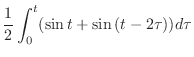 |
||
 |
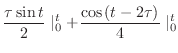 |
||
 |
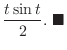 |
|
定理 5..9 (合成法則)
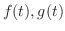 が区分的に連続な関数で,指数位数の関数ならば, が区分的に連続な関数で,指数位数の関数ならば,
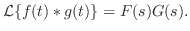
|
証明
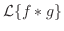 |
 |
![$\displaystyle \int_{0}^{\infty}e^{-st}[\int_{0}^{t}f(t-\tau)g(\tau)d\tau]dt$](img1659.png) |
|
 |
![$\displaystyle \int_{0}^{\infty}e^{-st}[\int_{0}^{\infty}u_{\tau}(t)f(t-\tau)g(\tau)d\tau]dt$](img1660.png) |
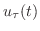 を挿入することにより無限積分に拡張された.
次に積分順序の交換を行なうと
を挿入することにより無限積分に拡張された.
次に積分順序の交換を行なうと
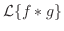 |
 |
![$\displaystyle \int_{0}^{\infty}g(\tau)[\int_{0}^{\infty}u_{\tau}(t)e^{-st}f(t-\tau)dt]d\tau$](img1662.png) |
|
 |
![$\displaystyle \int_{0}^{\infty}[e^{-\tau s}F(s)]d\tau$](img1663.png) |
||
 |
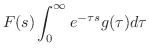 |
||
 |
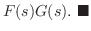 |
|
系 5..2
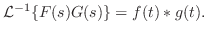
|
この定理より証明を引き伸ばしてきた積分法則の証明が示せます.
|
系 5..3
 が区分的に連続で指数位数の関数ならば が区分的に連続で指数位数の関数ならば
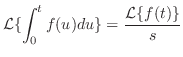
|
証明
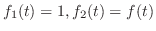 とおくと,合成法則より
とおくと,合成法則より
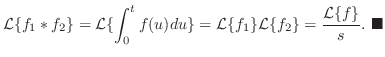
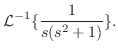
解
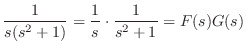
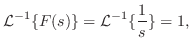
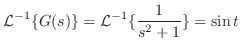
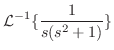 |
 |
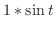 |
|
 |
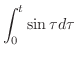 |
||
 |
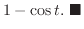 |
最後に合成法則の積分方程式(integral equation)への応用を紹介しましょう.積分方程式とは未知関数として積分を含んだ方程式のことです.
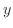 を求めよ.
を求めよ.
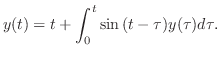
解 両辺にラプラス変換を施すと,
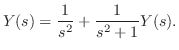
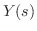 について解くと,
について解くと,