Next: 演習問題5.3.2 Up: ラプラス変換(The Laplace transformation) Previous: 演習問題5.3.1 目次 索引
|
定理 5..5 (微分法則)
 は は
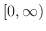 で連続で,指数位数の関数とする.さらに で連続で,指数位数の関数とする.さらに が が
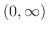 で区分的に連続ならば で区分的に連続ならば
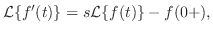
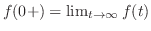 . . |
証明 定義より
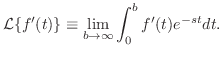
![$[0,b]$](img1441.png) を
を
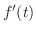 が不連続な点
が不連続な点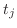 で分割する.
で分割する.
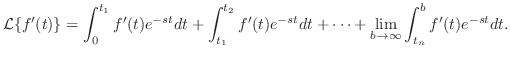
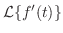 |
 |
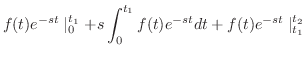 |
|
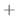 |
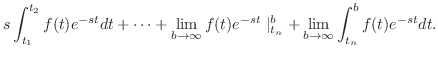 |
 は連続なので
は連続なので
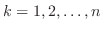 において,
において,
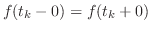 .よって
.よって
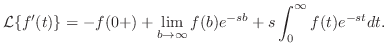
 は指数位数より,
は指数位数より,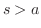 のとき第2項は0.したがって
のとき第2項は0.したがって
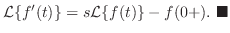
上の定理を繰り返し適用することにより,次の公式を得ることができます.
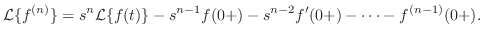
|
定理 5..6 (積分法則)
 が区分的に連続で指数位数の関数ならば が区分的に連続で指数位数の関数ならば
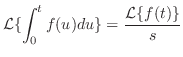
|
証明
( が連続の場合)
が連続の場合)
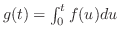 とおくと,
とおくと,
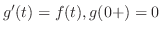 . また
. また は指数位数の関数より,
は指数位数の関数より,
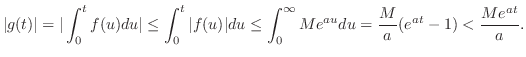
 も指数位数の関数となり,微分法則を用いると,
も指数位数の関数となり,微分法則を用いると,
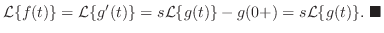
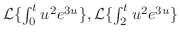 を求めよ.
を求めよ.
解
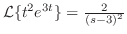 より
より
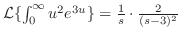 . 次に
. 次に
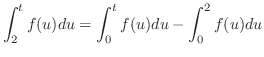
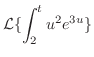 |
 |
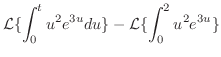 |
|
 |
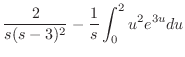 |
||
 |
![$\displaystyle \frac{2}{s(s-3)^2} - \frac{1}{s}[e^{3u}(\frac{u^2}{3} - \frac{2u}{9} + \frac{2}{27})]\mid_{0}^{2}$](img1466.png) |
||
 |
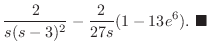 |
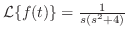 のとき
のとき を求めよ.
を求めよ.
解
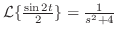 .積分法則より
.積分法則より
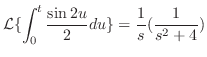
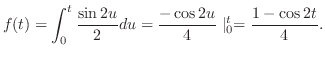
別解
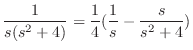
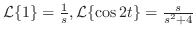 より
より
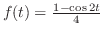 となる.
となる.

|
定理 5..7
 は区分的に連続で指数位数 は区分的に連続で指数位数 の関数とする. の関数とする.
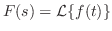 ならば ならば
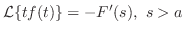
|
証明
定義より
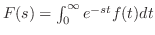 .
.  は指数位数より
は指数位数より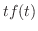 も指数位数となり,
も指数位数となり,
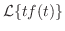 は存在する.また
は存在する.また は区分的に連続なので微分と積分の順序の交換が可能である.したがって,
は区分的に連続なので微分と積分の順序の交換が可能である.したがって,
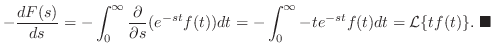
上の定理をくり返し適用すれば,次の系が得られます.
|
系 5..1
 は区分的に連続で指数位数 は区分的に連続で指数位数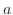 の関数とする. の関数とする.
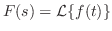 ならば ならば
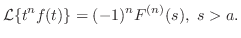
|
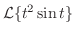 を求めよ.
を求めよ.
解
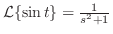 .よって
.よって
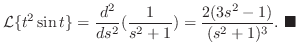
![${\cal L}\{f(t)\} = \log{[\frac{s+2}{s-3}]} = F(s)$](img1484.png) のとき
のとき を求めよ.
を求めよ.
解
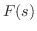 は私たちが知っている関数のラプラス変換に似ていません.そこで
は私たちが知っている関数のラプラス変換に似ていません.そこで
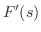 を考えて見ます.
を考えて見ます.
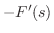 |
 |
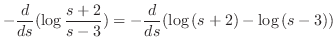 |
|
 |
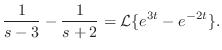 |
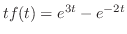 . したがって,
. したがって,
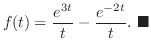
図5.3,5.4,5.5のような関数を周期関数(periodic function)といいます.周期関数のラプラス変換は次の定理より簡単に求めることができます.
|
定理 5..8
 が周期 が周期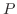 の区分的に連続な関数ならば,つまり の区分的に連続な関数ならば,つまり
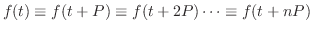 ならば ならば
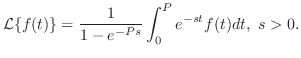
|
証明
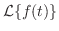 |
 |
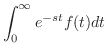 |
|
 |
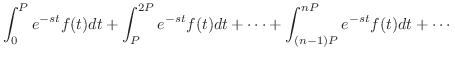 |
||
 |
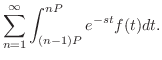 |
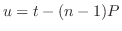 とおくと
とおくと
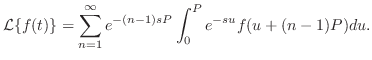
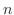 において
において
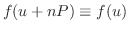 が成り立つことに注意すると
が成り立つことに注意すると
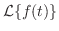 |
 |
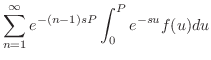 |
|
 |
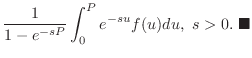 |
解
(a) 関数 は,区間
は,区間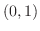 で
で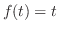 の周期1の関数より
の周期1の関数より
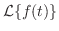 |
 |
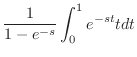 |
|
 |
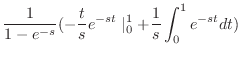 |
||
 |
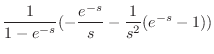 |
||
 |
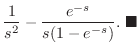 |
(b) 関数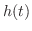 は,区間
は,区間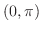 で
で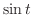 ,区間
,区間
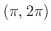 で0の周期
で0の周期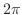 の関数だから
の関数だから
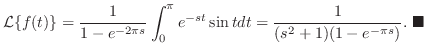
(c) 関数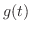 は,
は,
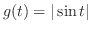 .また
.また
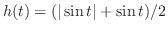 より
より
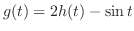 .したがって
.したがって
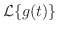 |
 |
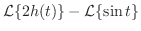 |
|
 |
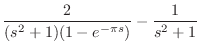 |
||
 |
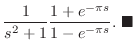 |
ここまでに扱った法則をまとめてみると次のような表5.2にすることができます.これらはラプラス変換の一般的な性質ですので次に進む前に各自使えるようにしておいて下さい.
この節を閉じる前にラプラス変換の有用性について述べておきます.そのための例として,上に掲げたラプラス変換の性質をもちいて初期値問題の解のラプラス変換を求めてみます.
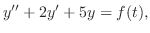
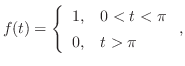
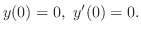
解 両辺にラプラス変換を施すと,
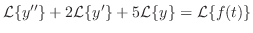
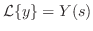 とおき,微分法則を用いると,
とおき,微分法則を用いると,
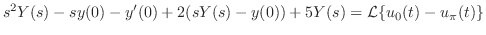
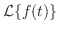 を計算すると
を計算すると
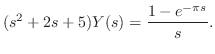
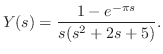
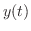 のラプラス変換です.
のラプラス変換です.
