Next: 演習問題5.2 Up: ラプラス変換(The Laplace transformation) Previous: 演習問題5.1 目次 索引
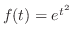 のラプラス変換は存在しません.なぜなら
のラプラス変換は存在しません.なぜなら
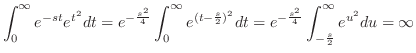
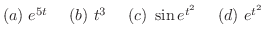
解
(a) 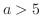 のとき
のとき
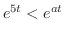 ,よって
,よって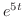 は指数位数
は指数位数
(b) 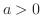 のとき
のとき
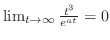 ,よって
,よって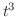 は指数位数.
は指数位数.
(c)
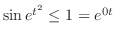 より
より
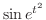 は指数位数.
は指数位数.
(d)
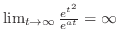 より,
より,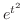 は指数位数でない.
は指数位数でない.

|
定義 5..3
[区分的に連続]
有限な区間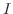 で定義された関数 で定義された関数 が次の条件を満たすとき, が次の条件を満たすとき, は区間 は区間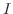 で区分的に連続(piecewise continuous function)であるという. で区分的に連続(piecewise continuous function)であるという.
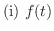 は区間 は区間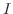 で有限個の点を除いて連続である. で有限個の点を除いて連続である.
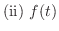 の不連続点 の不連続点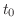 では,左側および右側極限値が存在する. では,左側および右側極限値が存在する.
|
|
定理 5..1 任意の
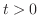 に対して,関数 に対して,関数 が区間 が区間![$[0,t]$](img1359.png) で区分的に連続かつ指数位数 で区分的に連続かつ指数位数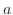 ならば, ならば, のラプラス変換は存在する. のラプラス変換は存在する. |
証明
 は指数位数
は指数位数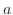 より,
より,
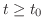 のとき
のとき
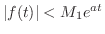
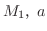 が存在する.また
が存在する.また は区分的に連続より,
は区分的に連続より,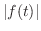 は
は![$[0,t_{0}]$](img1363.png) で有界.よって
で有界.よって
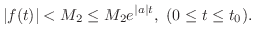
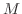 を
を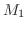 と
と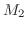 の大きい方とすると
の大きい方とすると
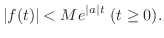
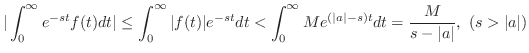
 のラプラス変換は存在する.
のラプラス変換は存在する.
