Next: 演習問題4.3 Up: 級数による解法(infinite series methods) Previous: 演習問題4.2 目次 索引
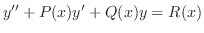
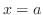 が特異点のとき,
が特異点のとき,
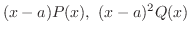
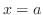 でともに解析的であるとき,
でともに解析的であるとき,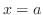 は確定特異点(regular singular point)といい,それ以外は不確定特異点(irregular singular point)といいます.
は確定特異点(regular singular point)といい,それ以外は不確定特異点(irregular singular point)といいます.
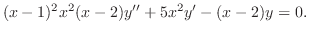
解
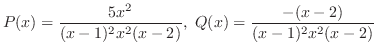
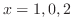 は特異点.次に
は特異点.次に
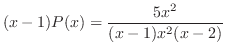
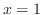 は不確定特異点.他の2つの特異点は確定特異点.
は不確定特異点.他の2つの特異点は確定特異点.

通常点のときと同様,確定特異点のまわりにも級数解が存在します.
|
定理 4..7 2階線形微分方程式
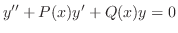
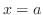 が確定特異点であるとき, が確定特異点であるとき,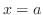 のまわりで のまわりで
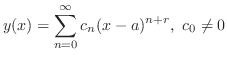
|
この級数
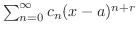 はFrobenius級数(Frobinius series)とよばれ,この級数を解として
はFrobenius級数(Frobinius series)とよばれ,この級数を解として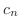 を求める方法をFrobenius法といいます.次の例題でFrobenius法の用い方を説明します.
を求める方法をFrobenius法といいます.次の例題でFrobenius法の用い方を説明します.
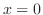 のまわりでの級数解を求めよ.
のまわりでの級数解を求めよ.
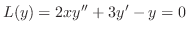
解
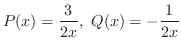
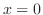 は確定特異点.よって解を
は確定特異点.よって解を
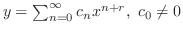 とおく.これを微分することにより得られる
とおく.これを微分することにより得られる
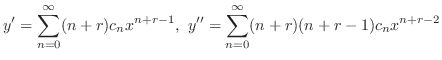
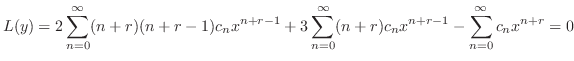
 のベキを必ず一番小さいものにそろえると
のベキを必ず一番小さいものにそろえると
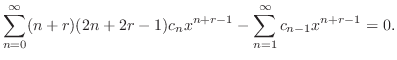
![$\displaystyle \underbrace{r(2r-1)c_{0}x^{r-1}}_{n = 0} + \sum_{n=1}^{\infty}[(n+r)(2n+2r+1)c_{n} - c_{n-1}]x^{n+r-1} = 0 $](img1184.png)
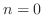 のときでてきた方程式
のときでてきた方程式
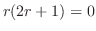 を決定方程式(indicial equation)という.この方程式を解くと
を決定方程式(indicial equation)という.この方程式を解くと
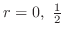 .
これより2つの一次独立な級数解
.
これより2つの一次独立な級数解
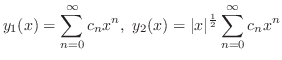
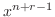 の係数を0とおくと漸化式
の係数を0とおくと漸化式
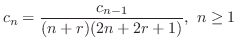
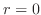 とおくと
とおくと
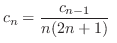 より
より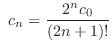
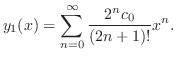
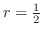 とおくと
とおくと
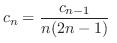 より
より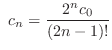
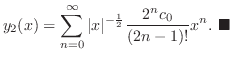
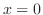 のまわりでの級数解をひとつ求めよ.
のまわりでの級数解をひとつ求めよ.
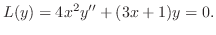
解
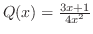 より
より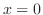 は確定特異点.そこで
は確定特異点.そこで
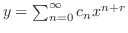 とおくと,
とおくと,
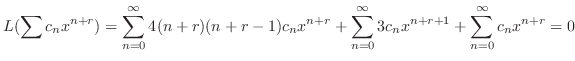
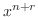 でそろえると,
でそろえると,
![$\displaystyle \sum_{n=0}^{\infty}[4(n+r)(n+r-1) + 1]c_{n}x^{n+r} + \sum_{n=1}^{\infty}3c_{n-1}x^{n+r} = 0. $](img1204.png)
![$\displaystyle \underbrace{(4r(r-1) + 1)c_{0}x^{r}}_{n = 0} + \sum_{n=1}^{\infty}\{[4(n+r)(n+r-1) + 1]c_{n} + 3c_{n-1}\}x^{n+r} = 0 $](img1205.png)
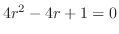 となるので,
となるので,
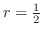 .また漸化式
.また漸化式
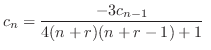 より
より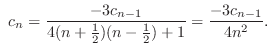
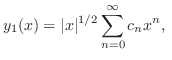 ただし
ただし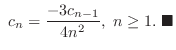
上の例題の解答は完全でありません.一次独立な解が2つあるはずです.ではもうひとつの解はどうやったら求まるのでしょうか.すでに学びましたが,ひとつの解がわかっているときは,階数低減法を用いてもうひとつの解を求めることができます.ここでは証明しませんが,もうひとつの解は次のように表わされることがわかっています.
|
定理 4..8 2階線形微分方程式
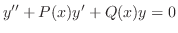
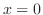 が確定特異点で,決定方程式の解 が確定特異点で,決定方程式の解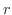 が重解のとき,1次独立な2つの解 が重解のとき,1次独立な2つの解
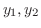 は次の形で与えられる. は次の形で与えられる.
|
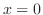 のまわりでの級数解を求めよ.
のまわりでの級数解を求めよ.
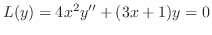
解
上の例題で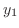 はすでに求めたので,
はすでに求めたので,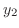 を求める.定理より,
を求める.定理より,
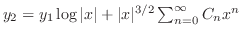 の形をした解を探す.計算の都合上
の形をした解を探す.計算の都合上
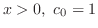 とおく.
とおく.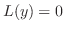 に
に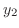 を代入すると
を代入すると
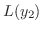 |
 |
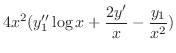 |
|
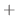 |
 |
||
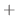 |
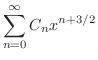 |
||
 |
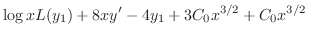 |
||
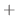 |
![$\displaystyle \sum_{n=1}^{\infty}[4(n + \frac{3}{2})(n + \frac{1}{2})C_{n} + C_{n} + 3C_{n-1}]x^{n+3/2} = 0$](img1223.png) |
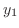 の最初の何項かを表わすと
の最初の何項かを表わすと
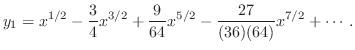
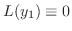 を用いると
を用いると
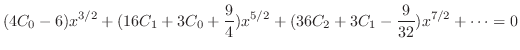
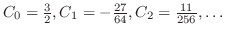 . よって
. よって
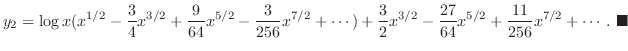
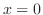 のまわりでの級数解を求めよ.
のまわりでの級数解を求めよ.
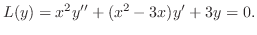
解
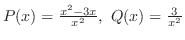 より
より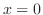 は確定特異点.そこで
は確定特異点.そこで
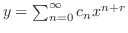 とおくと
とおくと
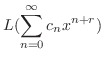 |
 |
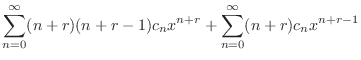 |
|
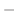 |
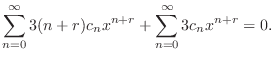 |
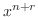 でそろえると
でそろえると
![$\displaystyle \sum_{n=0}^{\infty}[(n+r)(n+r-1) - 3(n+r) + 3]c_{n}x^{n+r} + \sum_{n=1}^{\infty}(n+r-1)c_{n-1}x^{n+r} = 0. $](img1235.png)
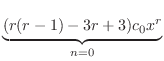 |
|||
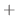 |
![$\displaystyle \sum_{n=1}^{\infty}\{[(n+r)(n+r-1) - 3(n+r) + 3]c_{n} + (n+r-1)c_{n-1}\}x^{n+r} = 0$](img1237.png) |
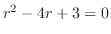 より
より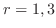 .よって2つの解
.よって2つの解
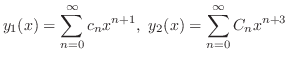
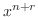 の係数を0とおくことより,漸化式
の係数を0とおくことより,漸化式
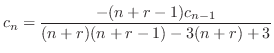
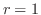 のとき
のとき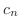 を求めると
を求めると
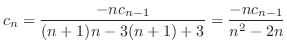
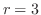 のとき
のとき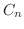 を求めると
を求めると
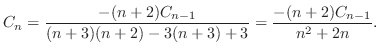
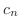 と
と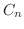 はよく見ると
はよく見ると
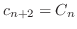 .つまり
.つまり
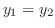 .
そこでもうひとつ一次独立な解を探さなければならない.そのために次のような定理がある.
.
そこでもうひとつ一次独立な解を探さなければならない.そのために次のような定理がある.
|
定理 4..9 2階線形微分方程式
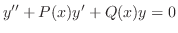
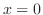 が確定特異点で,決定方程式の解 が確定特異点で,決定方程式の解
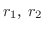 の差が正の整数のとき,1次独立な2つの解 の差が正の整数のとき,1次独立な2つの解
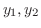 は次の形で与えられる. は次の形で与えられる.
|
これより上の例題のもうひとつの解は
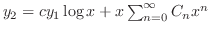 を
を
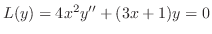 に代入することにより求めることができる.
に代入することにより求めることができる.
