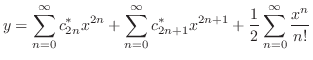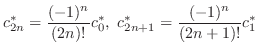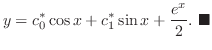Next: 演習問題4.2 Up: 級数による解法(infinite series methods) Previous: 演習問題4.1 目次 索引
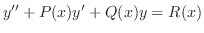
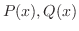 および
および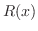 が点
が点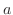 で解析的なとき,点
で解析的なとき,点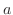 を通常点(ordinary point)といいます.通常点では次の定理が成り立ちます.
を通常点(ordinary point)といいます.通常点では次の定理が成り立ちます.
|
定理 4..6 2階線形微分方程式
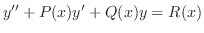
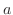 が通常点ならば,任意の定数 が通常点ならば,任意の定数
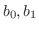 に対して,初期条件 に対して,初期条件
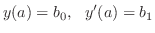
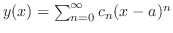 がただひとつ存在する. がただひとつ存在する. |
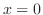 のまわりでの整級数解を求めよ.
のまわりでの整級数解を求めよ.
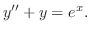
解
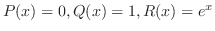 より,
より,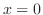 は通常点.よって,解を
は通常点.よって,解を
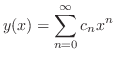
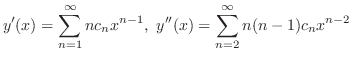
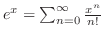 より,これらを与えられた方程式に代入すると
より,これらを与えられた方程式に代入すると
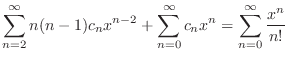
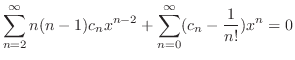
 のベキが
のベキが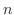 になるようにそろえると,
になるようにそろえると,
![$\displaystyle \sum_{n=0}^{\infty}[(n+2)(n+1)c_{n+2} + c_{n} - \frac{1}{n!}]x^{n} = 0 $](img1146.png)
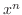 の係数はすべて0になる.よって漸化式
の係数はすべて0になる.よって漸化式
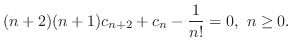
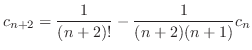
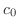 と
と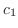 は初期条件
は初期条件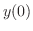 と
と
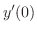 で決まるので,この場合は任意の定数と考えられる.よって,
で決まるので,この場合は任意の定数と考えられる.よって,
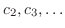 を順次求めると
を順次求めると
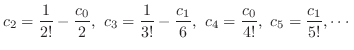
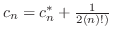 とおくと,漸化式は
とおくと,漸化式は
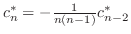 .
.
これを
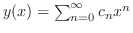 に代入すると
に代入すると