Next: 演習問題3.2 Up: 連立線形微分方程式(systems of linear differential Previous: 演習問題3.1 目次 索引
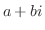 が微分方程式
が微分方程式
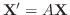 の特性方程式の根ならば,
の特性方程式の根ならば,
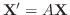 は
は
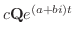 の形をした解をもっているはずです.ただし,
の形をした解をもっているはずです.ただし,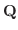 は複素固有ベクトル,
は複素固有ベクトル,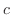 は任意の複素定数です.
は任意の複素定数です.
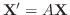 の
の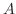 が実行列のとき,複素指数や複素ベクトルの存在は扱いにくいものです.とくに初期値
が実行列のとき,複素指数や複素ベクトルの存在は扱いにくいものです.とくに初期値
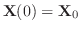 が実数のときはなおさらです.そこで解を実数と実関数だけで表わす必要があります.
が実数のときはなおさらです.そこで解を実数と実関数だけで表わす必要があります.
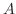 を実行列,
を実行列,
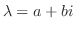 が複素固有値で
が複素固有値で
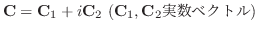 が
が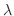 に対する固有ベクトルだとすると固有方程式(eigenequation)
に対する固有ベクトルだとすると固有方程式(eigenequation)
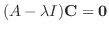
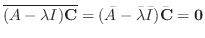
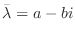 も固有値となり,対応する固有ベクトル
も固有値となり,対応する固有ベクトル
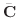 をもちます.したがって,
をもちます.したがって,
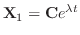 と
と
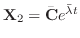 はともに
はともに
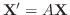 の解になります.もちろん
の解になります.もちろん
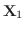 と
と
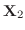 の一次結合も解です.とくにその中でも
の一次結合も解です.とくにその中でも
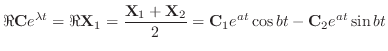
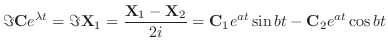
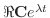 と
と
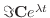 のことを,複素数
のことを,複素数
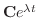 の実部(real part)と虚部(imaginary part)といいます.
の実部(real part)と虚部(imaginary part)といいます.
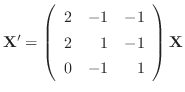 を解け.
を解け.
解
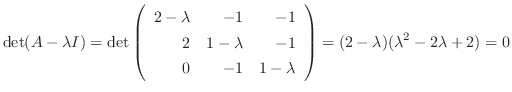
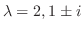 を得る.
を得る.
まず,固有値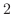 に対応する固有ベクトルを求めると
に対応する固有ベクトルを求めると
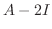 |
 |
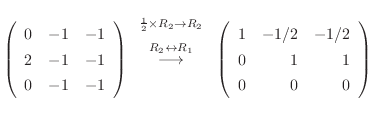 |
|
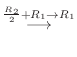 |
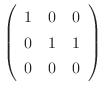 |
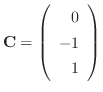 である.
である.
次に固有値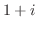 に対応する固有ベクトルを求める.
に対応する固有ベクトルを求める.
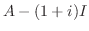 |
 |
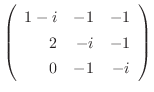 |
|
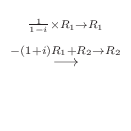 |
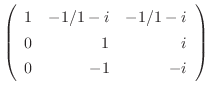 |
||
 |
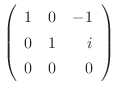 |
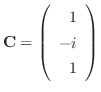 である.これより
である.これより
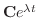 の実部と虚部を求めると,
の実部と虚部を求めると,
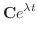 |
 |
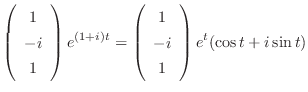 |
|
 |
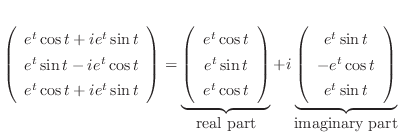 |
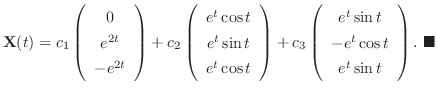
さて,行列 の特性方程式が重根をもつ場合はどうでしょう.この場合も,
の特性方程式が重根をもつ場合はどうでしょう.この場合も, が対角化可能(つまり,重複度と同数の一次独立な固有ベクトルをもつ)ならば,単根のときと同じように一般解を求めることができます.では
が対角化可能(つまり,重複度と同数の一次独立な固有ベクトルをもつ)ならば,単根のときと同じように一般解を求めることができます.では が対角化不可能の場合はどうでしょう.こんな場合に便利な方法として行列の指数関数を用いる方法があります.
が対角化不可能の場合はどうでしょう.こんな場合に便利な方法として行列の指数関数を用いる方法があります.
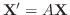 の解として,
の解として,
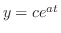 が
が
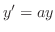 の解であったように,
の解であったように,
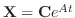 を考えます.ただし
を考えます.ただし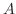 は
は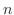 次の正方行列,
次の正方行列,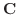 は定数ベクトルです.これが可能なためには
は定数ベクトルです.これが可能なためには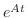 に意味づけを行なう必要があります.そこで
に意味づけを行なう必要があります.そこで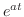 のMaclaurin級数
のMaclaurin級数
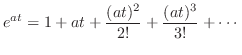
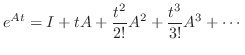
 で収束することが知られています.これを行列
で収束することが知られています.これを行列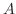 の指数行列(exponential matrix)といいます.また
の指数行列(exponential matrix)といいます.また
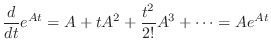
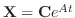 は
は
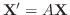 の解といえます.
の解といえます.
ここでひとつ問題があります.それは,どうやって
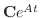 を計算するかということです.定義を使うと無限級数の計算をすることになりますが,じつは無限級数の計算をせずに,解を求める方法があるのです.まず
を計算するかということです.定義を使うと無限級数の計算をすることになりますが,じつは無限級数の計算をせずに,解を求める方法があるのです.まず
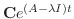 の展開を考えて下さい.つまり,
の展開を考えて下さい.つまり,
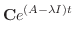 |
 |
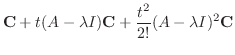 |
|
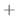 |
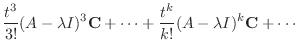 |
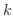 で
で
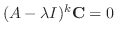 が成り立てば,上の展開で
が成り立てば,上の展開で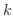 の後はすべて0になります.よってこのときは,有限級数の計算をすればよいことになります.
の後はすべて0になります.よってこのときは,有限級数の計算をすればよいことになります.
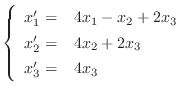 を解け.
を解け.
解
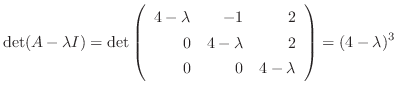
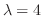 である.次に固有値
である.次に固有値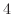 に対する固有ベクトルCを求める.
に対する固有ベクトルCを求める.
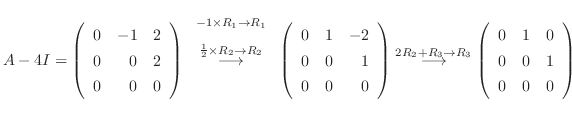
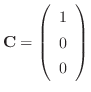 となり,ひとつの解
となり,ひとつの解
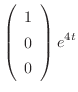
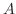 は三次の正方行列なので一般解を表わすには,
は三次の正方行列なので一般解を表わすには,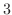 つの一次独立な解が必要である.そこで
つの一次独立な解が必要である.そこで
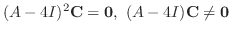
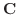 を見つける.
を見つける.
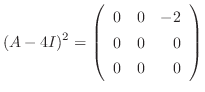
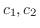 は任意の値を取ることができるので,
は任意の値を取ることができるので,
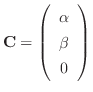 とおくと,
とおくと,
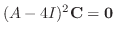 を満たす.次にもうひとつの条件
を満たす.次にもうひとつの条件
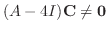 を満たすように
を満たすように
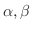 を選ぶと,
を選ぶと,
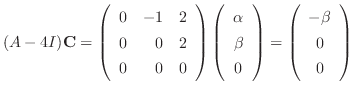
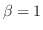 .よって
.よって
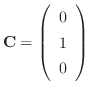 となり,2つめの解
となり,2つめの解
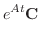 |
 |
![$\displaystyle e^{4t}e^{(A - 4I)t}{\bf C} = e^{4t}[{\bf C} + t(A - 4I){\bf C}]$](img955.png) |
|
 |
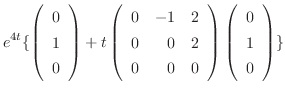 |
||
 |
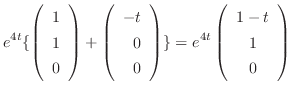 |
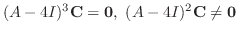
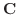 を見つける.
を見つける.
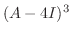 は零行列なので
は零行列なので
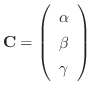 は
は
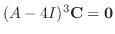 を満たす.ここでもうひとつの条件を用い,前に選んだ
を満たす.ここでもうひとつの条件を用い,前に選んだ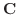 と一次独立になるように,
と一次独立になるように,
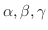 を選ぶと,
を選ぶと,
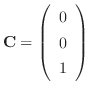 となる.これより3つめの解を計算すると
となる.これより3つめの解を計算すると
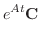 |
 |
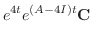 |
|
 |
![$\displaystyle e^{4t}[{\bf C} + t(A - 4I){\bf C} + \frac{t^{2}}{2!}(A - 4I)^{2}{\bf C}]$](img965.png) |
||
 |
![$\displaystyle e^{4t}[\left(\begin{array}{c}
0\\
0\\
1
\end{array}\right) + t\...
...
0&0&0
\end{array}\right)\left(\begin{array}{c}
0\\
0\\
1
\end{array}\right)]$](img966.png) |
||
 |
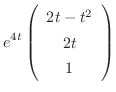 |
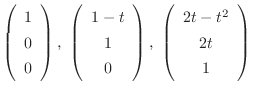 は一次独立なので,一般解は
は一次独立なので,一般解は
![$\displaystyle {\bf X} = e^{4t}[c_{1}\left(\begin{array}{c}
1\\
0\\
0
\end{arr...
...right) + c_{3}\left(\begin{array}{c}
2t - t^{2}\\
2t\\
1
\end{array}\right)] $](img969.png)
