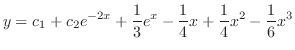Next: 演習問題2.4 Up: 線形微分方程式(linear differential equations) Previous: 演習問題2.3 目次 索引
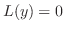 について学びました.ここでは定数係数の非同次線形微分方程式
について学びました.ここでは定数係数の非同次線形微分方程式
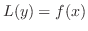 の特殊解の求め方について学びます.ただしここで扱う解法は
の特殊解の求め方について学びます.ただしここで扱う解法は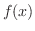 がある特殊な形,つまり同次線形微分方程式の解の形をしたものに限ります.
がある特殊な形,つまり同次線形微分方程式の解の形をしたものに限ります.
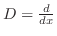 とおきます.すると
とおきます.すると
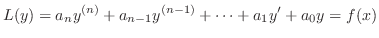
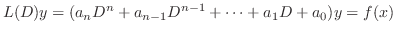
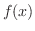 が同次線形微分方程式の解の形をしているとすると,
が同次線形微分方程式の解の形をしているとすると,
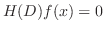 を満たす
を満たす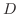 の多項式
の多項式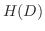 が存在します.そこでこの方程式の特殊解を
が存在します.そこでこの方程式の特殊解を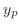 とすると
とすると
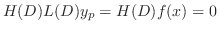
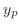 を見つけるには同次方程式
を見つけるには同次方程式
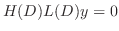
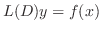
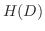 をあげておきます.
をあげておきます.
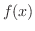 |
 |
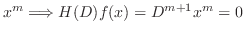 |
|
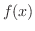 |
 |
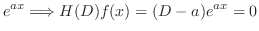 |
|
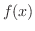 |
 |
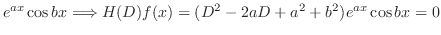 |
|
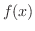 |
 |
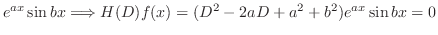 |
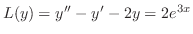 を解け.
を解け.
解
補助方程式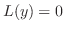 の特性方程式は
の特性方程式は
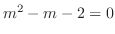 より特性根
より特性根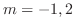 を得る.よって余関数
を得る.よって余関数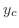 は
は
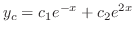
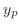 を未定係数法を用いて求める.
を未定係数法を用いて求める.
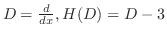 とおくと,
とおくと,
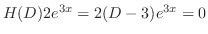 より求める特殊解
より求める特殊解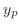 は
は
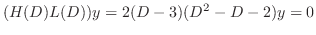
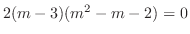 より基本解は
より基本解は
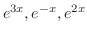 である.よって
である.よって
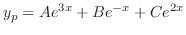
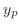 は
は
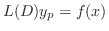 を満たさなければならないので
を満たさなければならないので
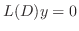 を満たす
を満たす
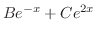 は省いてもよい.したがって特殊解
は省いてもよい.したがって特殊解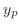 の形を
の形を
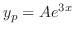
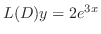 に代入すると
に代入すると
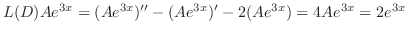
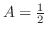 .これより特殊解
.これより特殊解
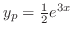 を得る.したがって一般解は
を得る.したがって一般解は
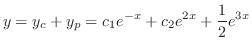

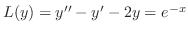 を解け.
を解け.
解
補助方程式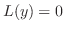 の特性方程式は
の特性方程式は
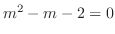 より特性根
より特性根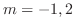 を得る.よって余関数
を得る.よって余関数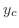 は
は
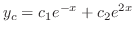
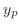 を未定係数法を用いて求める.
を未定係数法を用いて求める.
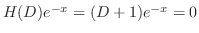 より,求める特殊解
より,求める特殊解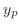 は
は
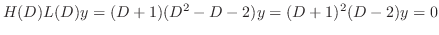
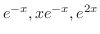 であるが,
であるが,
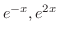 は余関数の解なので省くと
は余関数の解なので省くと
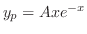
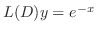 に代入すると
に代入すると
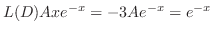
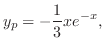
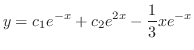

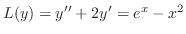 を解け.
を解け.
解
補助方程式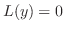 の特性方程式は
の特性方程式は
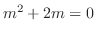 より特性根
より特性根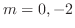 を得る.よって余関数
を得る.よって余関数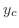 は
は
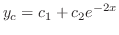
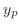 を未定係数法を用いて求めるには,重ね合わせの原理より
を未定係数法を用いて求めるには,重ね合わせの原理より
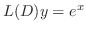 の特殊解
の特殊解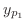 と
と
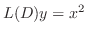 の特殊解
の特殊解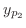 を求めれば
を求めれば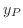 は
は
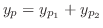 で与えられる.
で与えられる.
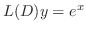 の特殊解
の特殊解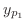 は
は
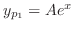 .また
.また
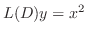 の特殊解
の特殊解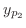 は
は
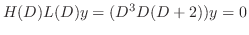
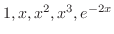 となるが,
となるが,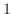 と
と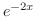 は余関数数の解なので省くと
は余関数数の解なので省くと
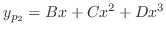
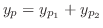 とおき,これを
とおき,これを
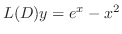 に代入すると
に代入すると
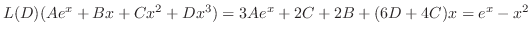 . したがって
. したがって
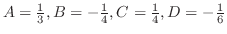 .よって一般解は
.よって一般解は