Next: 演習問題2.2 Up: 線形微分方程式(linear differential equations) Previous: 演習問題2.1 目次 索引
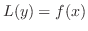 の係数が定数でないとき,一般解を求めるのは非常に難しかったり,不可能だったりします.ただ
の係数が定数でないとき,一般解を求めるのは非常に難しかったり,不可能だったりします.ただ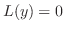 の解がひとつでもわかれば高階線形微分方程式
の解がひとつでもわかれば高階線形微分方程式
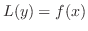 を少し簡単な形に直すことができます.わかりやすいように2階の線形微分方程式を用いて示しましょう.
を少し簡単な形に直すことができます.わかりやすいように2階の線形微分方程式を用いて示しましょう.
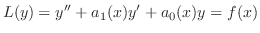
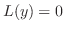 の0でない解
の0でない解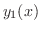 がわかっているとします.ここで
がわかっているとします.ここで
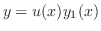 とおいて
とおいて
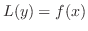 に代入すると
に代入すると
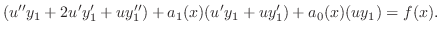
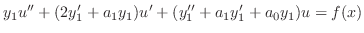
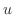 の係数は
の係数は
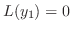 より0になることに注意して,
より0になることに注意して,
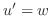 とおくと
とおくと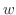 についての1階の線形微分方程式
についての1階の線形微分方程式
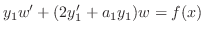
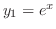 が
が
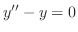 の解であることを利用して次の微分方程式を解け.
の解であることを利用して次の微分方程式を解け.
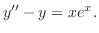
解
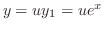 とおくと
とおくと
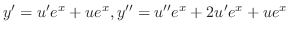 .
これらを
.
これらを
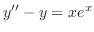 に代入すると
に代入すると
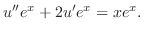
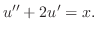
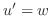 とおくと
とおくと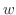 についての 1階の線形微分方程式
についての 1階の線形微分方程式
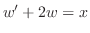
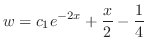
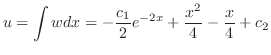
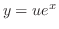 より一般解
より一般解
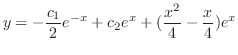

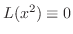 を用いて
を用いて
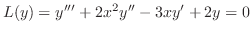
解
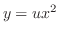 とおくと
とおくと
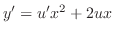 ,
,
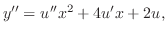
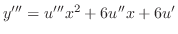 より
より
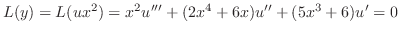
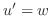 とおくと
とおくと