Next: 5.6 解答 Up: 演習問題解答 Previous: 5.4 解答 索引
5.5
1.
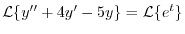
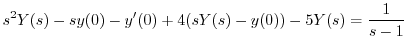
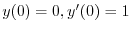 を代入すると
を代入すると
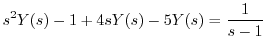
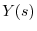 について解くと
について解くと
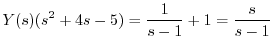
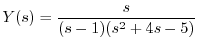
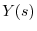 の逆変換を求めると
の逆変換を求めると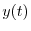 が得られる.つまり
が得られる.つまり
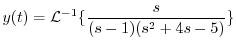
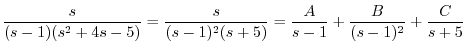
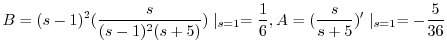
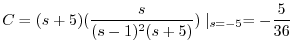
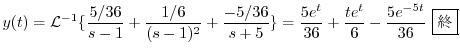
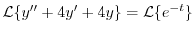
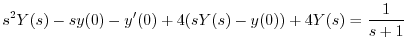
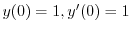 を代入すると
を代入すると
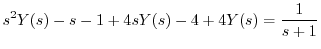
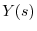 について解くと
について解くと
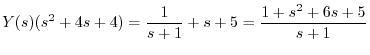
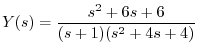
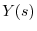 の逆変換を求めると
の逆変換を求めると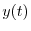 が得られる.つまり
が得られる.つまり
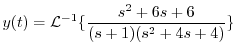
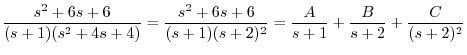
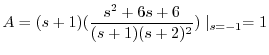
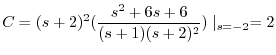
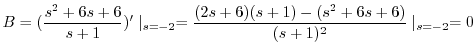
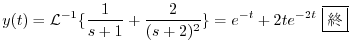
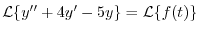
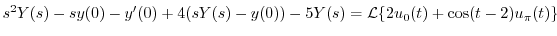
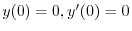 を代入すると
を代入すると
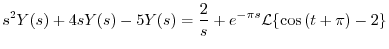
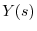 について解くと
について解くと
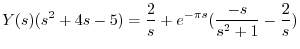
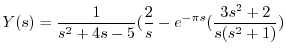
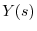 の逆変換を求めると
の逆変換を求めると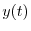 が得られる.つまり
が得られる.つまり
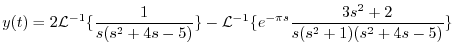
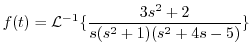
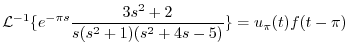
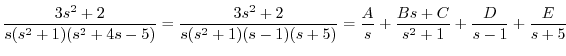
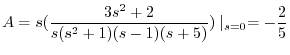
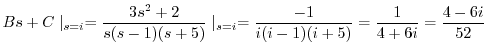
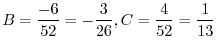
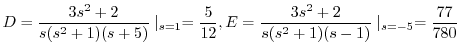
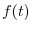 |
 |
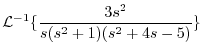 |
|
 |
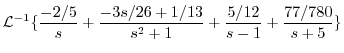 |
||
 |
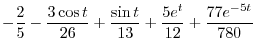 |
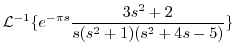 |
|||
 |
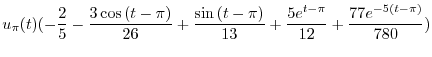 |
また
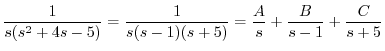
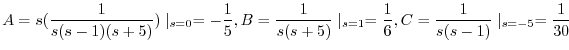
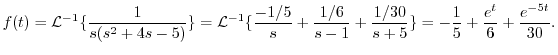
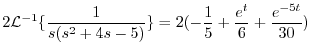
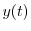 |
 |
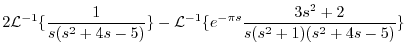 |
|
 |
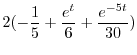 |
||
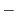 |
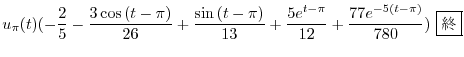 |
(d) 両辺にラプラス変換を施すと,
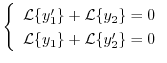
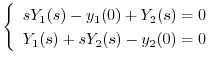
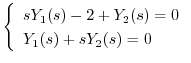
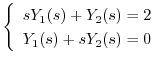
Cramerの公式を用いて
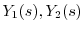 について解くと
について解くと
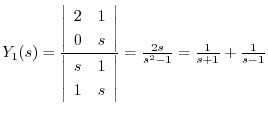
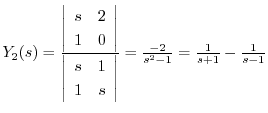
これより
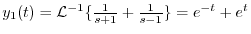
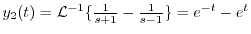

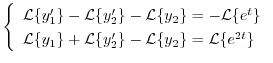
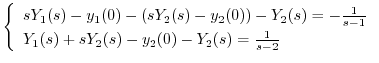
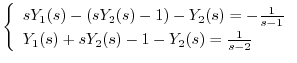
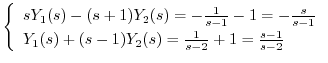
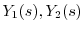 を求めると
を求めると
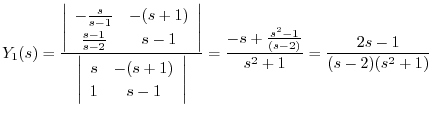
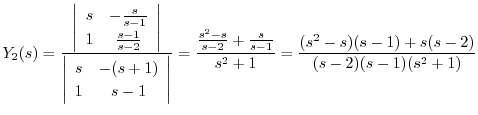
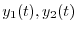 を求める.
を求める.
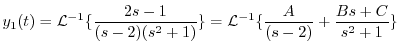
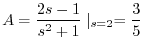
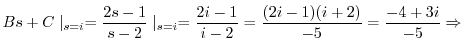
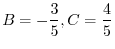
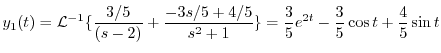
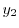 を求める.
を求める.
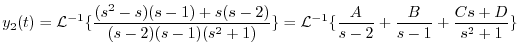
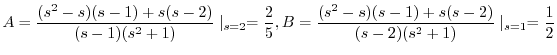
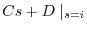 |
 |
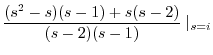 |
|
 |
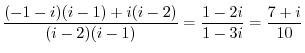 |
||
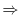 |
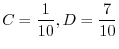 |
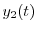 |
 |
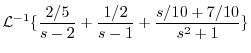 |
|
 |
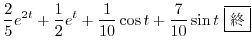 |
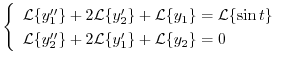
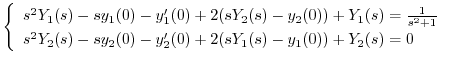
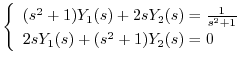
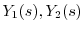 を求めると
を求めると
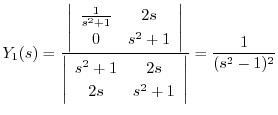
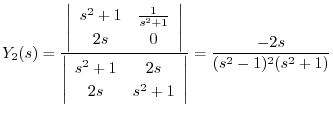
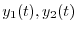 を求める.
を求める.
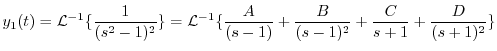
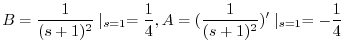
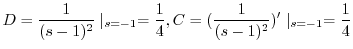
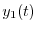 |
 |
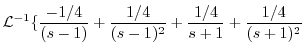 |
|
 |
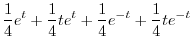 |
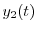 |
 |
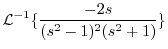 |
|
 |
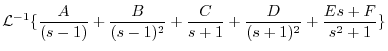 |
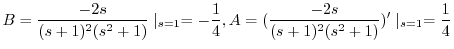
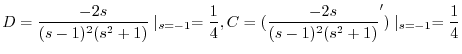
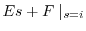 |
 |
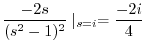 |
|
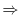 |
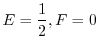 |
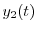 |
 |
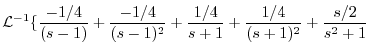 |
|
 |
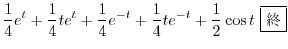 |