: 演習問題
: ラプラス変換
: 演習問題
目次
索引
ラプラス変換はどのような関数に対しても存在するわけではありません.たとえば,
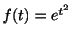 のラプラス変換は存在しません.なぜなら
ではどんなときラプラス変換は存在するのでしょうか.この疑問に答えるための準備として,次の定義をみてみましょう.
のラプラス変換は存在しません.なぜなら
ではどんなときラプラス変換は存在するのでしょうか.この疑問に答えるための準備として,次の定義をみてみましょう.
例題 5.8
次の関数のうち指数位数のものをあげよ.
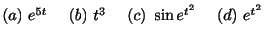
解
(a) 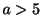 のとき
のとき
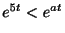 ,よって
,よって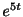 は指数位数
は指数位数
(b) 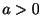 のとき
のとき
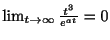 ,よって
,よって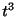 は指数位数.
は指数位数.
(c)
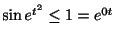 より
より
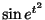 は指数位数.
は指数位数.
(d)
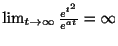 より,
より,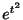 は指数位数でない.
は指数位数でない.
例題 5.9
下の図は区分的に連続な関数の一例です.
図 5.2:
区分的に連続な関数
![\begin{figure}\begin{center}
\includegraphics[width=8cm]{DFQ/Fig2.eps}
\end{center}\end{figure}](img1419.gif) |
証明
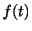 は指数位数
は指数位数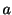 より,
より,
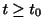 のとき
のとき
を満たす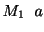 が存在する.また
が存在する.また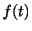 は区分的に連続より,
は区分的に連続より,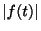 は
は![$ [0,t_{0}]$](img1425.gif) で有界.よって
で有界.よって
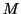 を
を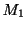 と
と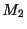 の大きい方とすると
これより
したがって,
の大きい方とすると
これより
したがって,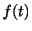 のラプラス変換は存在する.
のラプラス変換は存在する.
Administrator
平成26年9月18日
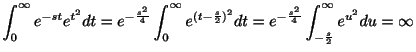
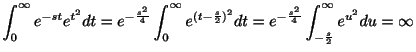
![]() のとき
のとき
![]() ,よって
,よって![]() は指数位数
は指数位数
![]() のとき
のとき
![]() ,よって
,よって![]() は指数位数.
は指数位数.
![]() より
より
![]() は指数位数.
は指数位数.
![]() より,
より,![]() は指数位数でない.
は指数位数でない.
![]()
![]() は指数位数
は指数位数![]() より,
より,
![]() のとき
のとき