




: 演習問題
: 級数による解法
: 級数による解法
目次
索引
私たちがここまで扱ってきた常微分方程式は,求積法により解が得られるものばかりでした.そこで,ここでは求積法で解を得るのが困難な場合や近似解を得たいとき用いられる級数による解法(infinite series method)を学びます.この方法は無限級数を与えられた微分方程式の解と考え,無限級数の係数を決めていくという方法で,じつは微分方程式を解くうえでもっとも初歩的な方法かも知れません.ただ,しばしば起きることですが,無限級数の係数をすべて決めるのが困難なことがよくあります.そんなときは,最初の何項かが解の近似として用いられることがよくあります.
まずは整級数の性質に関する基本的な定理について考えてみましょう.
各項が関数であるような級数を関数項級数(series of functions)といいます.
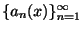 を区間
を区間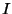 で定義された関数の列とします.この関数列
で定義された関数の列とします.この関数列
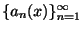 より
より
を考えます.区間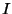 のすべての点
のすべての点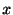 で数列
で数列
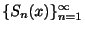 が収束するとき,つまり
であるような関数
が収束するとき,つまり
であるような関数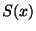 が存在するとき,級数
が存在するとき,級数
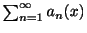 は収束するといい,
は収束するといい,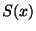 を無限級数の和とよびます.とくに収束が区間
を無限級数の和とよびます.とくに収束が区間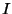 において一様収束である場合,つまり,区間
において一様収束である場合,つまり,区間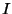 の任意の
の任意の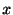 に対して
に対して
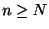
ならば
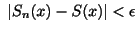
となる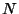 が区間
が区間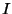 の
の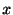 に無関係に存在する場合,級数
に無関係に存在する場合,級数
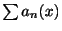 は区間
は区間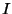 で一様収束する(uniformly convergent)といいます.
で一様収束する(uniformly convergent)といいます.
ここで
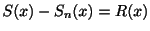 とおくと,無限級数の一様収束は次のように表わせます.つまり区間
とおくと,無限級数の一様収束は次のように表わせます.つまり区間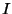 の任意の
の任意の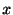 に対して
に対して
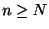
ならば
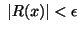
となる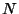 が存在します.
が存在します.
証明
ところで
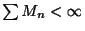 より,どんな
より,どんな
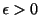 に対しても
に対しても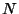 が存在し,
が存在し,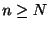 ならば
ここで
ならば
ここで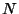 は明らかに
は明らかに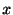 とは無関係なので,
とは無関係なので,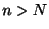 のとき
のとき
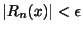 が成り立つ.
が成り立つ.
無限級数が一様収束するとき,級数は有限級数のもっている多くの性質を継承します.
無限級数
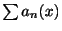 において,とくに
において,とくに
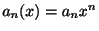 のときを整級数(power series)といいます.たとえば
のときを整級数(power series)といいます.たとえば
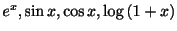 のTaylor級数
のTaylor級数
は整級数のひとつです.
さて
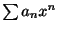 は
は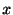 のどんな値に対して収束するのでしょうか.
のどんな値に対して収束するのでしょうか.
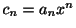 とおき,D'Alembertの判定法を用いると
とおき,D'Alembertの判定法を用いると
ここで
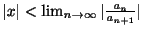 ならば
ならば
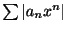 は収束し,
は収束し,
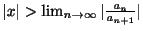 ならば
ならば
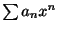 は発散するのでこの極限値
を収束半径(radius of convergence)といいます.
は発散するのでこの極限値
を収束半径(radius of convergence)といいます.
例題 4.1
次の整級数の収束半径を求めよ.
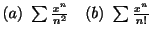
解
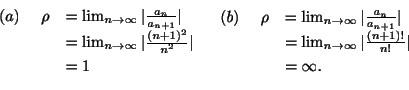
次に整級数の基本性質をあげておきます.
関数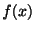 が正の収束半径をもつ整級数
が正の収束半径をもつ整級数
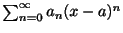 で表わされるとき,
で表わされるとき,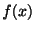 は点
は点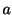 で解析的(analytic)であるといいます.また,開区間
で解析的(analytic)であるといいます.また,開区間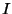 の各点で解析的な関数は区間
の各点で解析的な関数は区間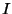 で解析的であるといいます.
で解析的であるといいます.





: 演習問題
: 級数による解法
: 級数による解法
目次
索引
Administrator
平成26年9月18日
![]() を区間
を区間![]() で定義された関数の列とします.この関数列
で定義された関数の列とします.この関数列
![]() より
より
![]() とおくと,無限級数の一様収束は次のように表わせます.つまり区間
とおくと,無限級数の一様収束は次のように表わせます.つまり区間![]() の任意の
の任意の![]() に対して
に対して
![]() において,とくに
において,とくに
![]() のときを整級数(power series)といいます.たとえば
のときを整級数(power series)といいます.たとえば
![]() のTaylor級数
のTaylor級数
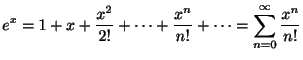
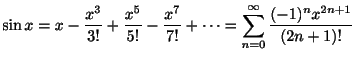
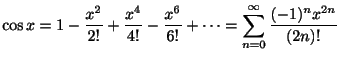
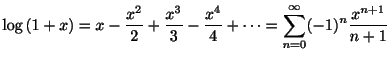
![]() は
は![]() のどんな値に対して収束するのでしょうか.
のどんな値に対して収束するのでしょうか.
![]() とおき,D'Alembertの判定法を用いると
とおき,D'Alembertの判定法を用いると
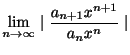
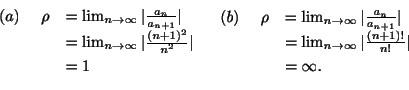
![]() が正の収束半径をもつ整級数
が正の収束半径をもつ整級数
![]() で表わされるとき,
で表わされるとき,![]() は点
は点![]() で解析的(analytic)であるといいます.また,開区間
で解析的(analytic)であるといいます.また,開区間![]() の各点で解析的な関数は区間
の各点で解析的な関数は区間![]() で解析的であるといいます.
で解析的であるといいます.