




: 連立線形微分方程式
: 線形微分方程式
: 演習問題
目次
索引
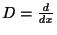 とおくと
は
と表せます.このとき,方程式
とおくと
は
と表せます.このとき,方程式
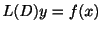 をみたすように関数
をみたすように関数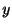 を対応させる演算素を,
を対応させる演算素を,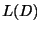 の逆演算子とよび,
と書き表します.つまり,
の逆演算子とよび,
と書き表します.つまり,
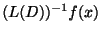 は,すべての関数
は,すべての関数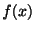 に対して,関係式
をみたすものとして定義します.
に対して,関係式
をみたすものとして定義します.
演算子法による計算法則
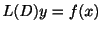 の特殊解を
の特殊解を
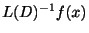 で計算しようというものであるから,
で計算しようというものであるから,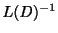 の性質を調べておく必要があります.
の性質を調べておく必要があります.
定理 2.8 (線形性)
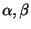
を定数,
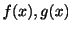
を関数とするとき,
証明 最初の式は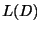 の定義から直ちにわかる.第2の等式は
の定義から直ちにわかる.第2の等式は
より明らかである.
定理 2.9 (基本公式)
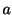
を定数,
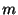
を自然数とするとき,
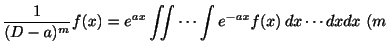
反復積分
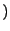
証明
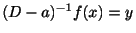 とすると,
とすると,
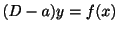 .すなわち
これは1階線形微分方程式なので,積分因子
.すなわち
これは1階線形微分方程式なので,積分因子
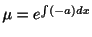 . これを両辺にかけると,
これより,
これを繰り返すと
. これを両辺にかけると,
これより,
これを繰り返すと
例題 2.19
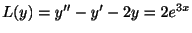
を解け.
解
補助方程式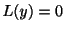 の特性方程式は
の特性方程式は
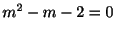 より特性根
より特性根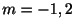 を得る.よって余関数
を得る.よって余関数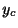 は
は
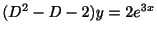 より,
よって
より,
よって
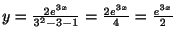 .これより特殊解
.これより特殊解
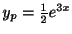 を得る.したがって一般解は
で与えられる.
を得る.したがって一般解は
で与えられる.
問 2.1
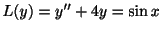
を解け.
解答 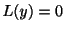 の特性方程式は
の特性方程式は
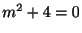 より,特性根
より,特性根
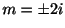 を得る.よって余関数
を得る.よって余関数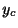 は
は
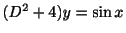 より,
より,
問 2.2
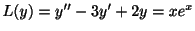
の特殊解を求めよ..
解答 特殊解を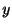 とすると,
とすると,





: 連立線形微分方程式
: 線形微分方程式
: 演習問題
目次
索引
Administrator
平成26年9月18日
![]() の特殊解を
の特殊解を
![]() で計算しようというものであるから,
で計算しようというものであるから,![]() の性質を調べておく必要があります.
の性質を調べておく必要があります.
![]() の定義から直ちにわかる.第2の等式は
の定義から直ちにわかる.第2の等式は
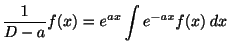
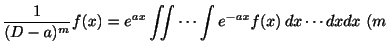 反復積分
反復積分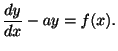
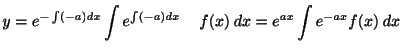
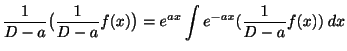
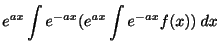
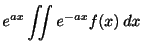
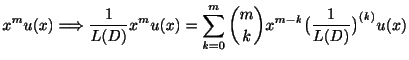
![]() の特性方程式は
の特性方程式は
![]() より特性根
より特性根![]() を得る.よって余関数
を得る.よって余関数![]() は
は
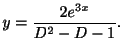
![]() の特性方程式は
の特性方程式は
![]() より,特性根
より,特性根
![]() を得る.よって余関数
を得る.よって余関数![]() は
は
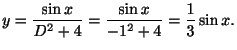
![]() とすると,
とすると,