Next: 索引 Up: 演習問題詳解 Previous: 5.2 留数 索引
1.
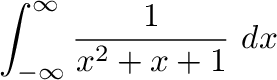
 を実軸上の
を実軸上の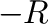 と
と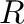 を結ぶ直線と
を結ぶ直線と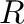 と
と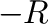 を結ぶ半径
を結ぶ半径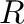 ,中心0の曲線
,中心0の曲線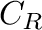 とすると,
とすると,
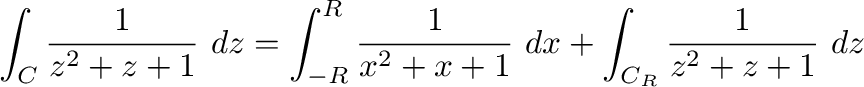
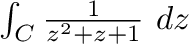 を求めると,特異点は
を求めると,特異点は
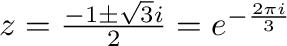 であるが,
であるが,
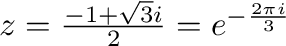 だけが曲線
だけが曲線 の内部にあるので,留数定理により
の内部にあるので,留数定理により
![$\displaystyle \int_{C}\frac{1}{(z^2 +1)(z^2 +4)}\ dz = 2\pi i(Res[e^{-\frac{2\pi i}{3}}])$](img1150.png)
![$\displaystyle Res[\frac{-1 + \sqrt{3}i}{2}]$](img1151.png) |
 |
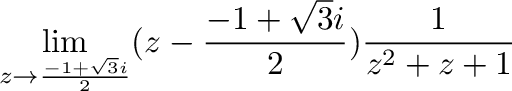 |
|
 |
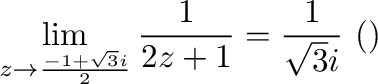 |
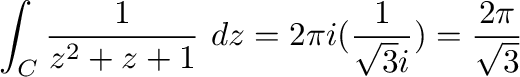
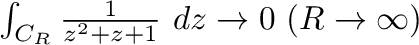 を示せれば,
を示せれば,
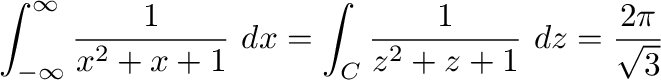
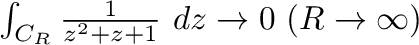 を示す.
を示す.

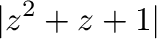 |
 |
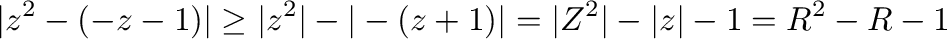 |
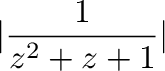 |
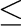 |
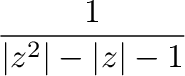 |
|
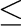 |
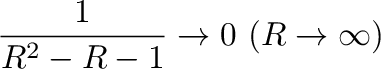 |
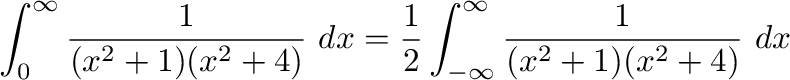
 を実軸上の
を実軸上の と
と を結ぶ直線と
を結ぶ直線と と
と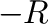 を結ぶ半径
を結ぶ半径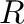 ,中心0の曲線
,中心0の曲線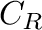 とすると,
とすると,
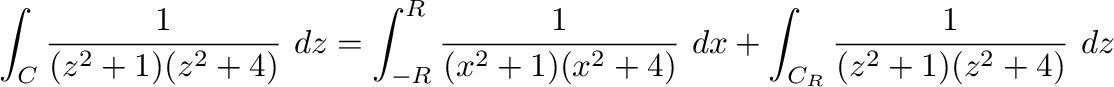
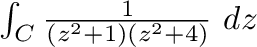 を求めると,特異点は
を求めると,特異点は
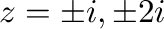 であるが,
であるが,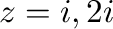 だけが曲線
だけが曲線 の内部にあるので,留数定理により
の内部にあるので,留数定理により
![$\displaystyle \int_{C}\frac{1}{(z^2 +1)(z^2 +4)}\ dz = 2\pi i(Res[i] + Res[2i])$](img1169.png)
![$\displaystyle Res[i] = \lim_{z \to i}(z - i)\frac{1}{(z^2 + 1)(z^2 + 4)} = \lim_{z \to i}\frac{1}{(z+i)(z^2 +4)} = \frac{1}{2i(3)} = \frac{1}{6i}$](img1170.png)
![$\displaystyle Res[2i] = \lim_{z \to 2i}(z - 2i)\frac{1}{(z^2 + 1)(z^2 + 4)} = \lim_{z \to 2i}\frac{1}{(z^2 + 1)(z + 2i)} = \frac{1}{-3(4i)} = \frac{-1}{12i}$](img1171.png)
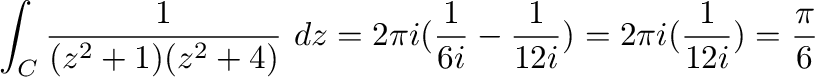
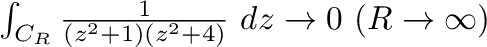 を示せれば,
を示せれば,
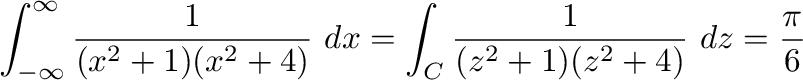
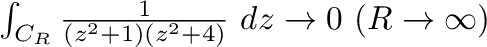 を示す.
を示す.
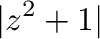 |
 |
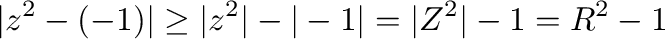 |
|
 |
 |
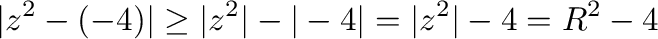 |
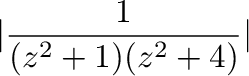 |
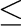 |
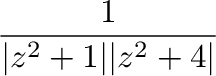 |
|
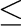 |
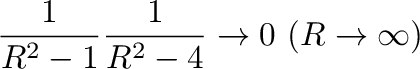 |