Next: 4.2 複素積分 Up: 演習問題詳解 Previous: 3.2 正則関数 索引
1. 複素積分を求めるには,一般に曲線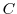 を
を
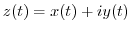 とパラメター化する.
とパラメター化する.
この曲線は点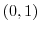 と点
と点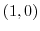 を結ぶ直線であるので,
を結ぶ直線であるので,
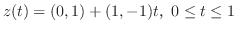 とパラメター化できる.したがって,
とパラメター化できる.したがって,
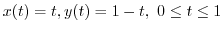 .
これより
.
これより
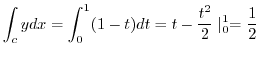
別解 この問題は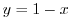 と
と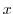 で表示されているので,直接積分できる.
で表示されているので,直接積分できる.
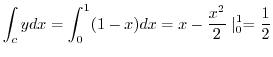
この曲線は点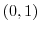 と点
と点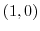 を結ぶ直線であるので,
を結ぶ直線であるので,
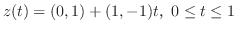 とパラメター化できる.したがって,
とパラメター化できる.したがって,
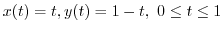 ,
, 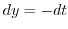 .
これより
.
これより
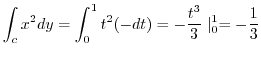
この曲線は点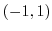 と点
と点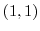 を
を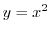 で結ぶ曲線であるので,
で結ぶ曲線であるので,
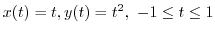 ,
, 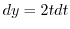 とパラメター化できる.これより
とパラメター化できる.これより
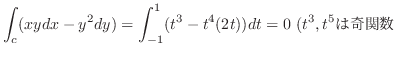
この曲線は中心を原点とする半径1の円であるので,
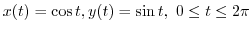 とパラメター化できる.
とパラメター化できる.
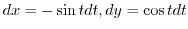 となるので
となるので
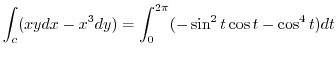
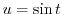 とおくと
とおくと
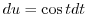 ,
,
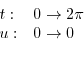 となるので
となるので
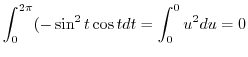
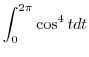 |
 |
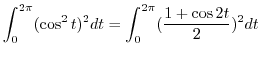 |
|
 |
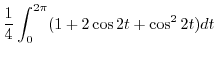 |
||
 |
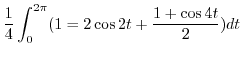 |
||
 |
![$\displaystyle \frac{1}{4}[\frac{3t}{2} + \cos{2t} + \frac{\sin{4t}}{8}\mid_{0}^{2\pi}]$](img578.png) |
||
 |
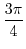 |
2.
(a) この曲線はすでにパラメター化されている.
したがって
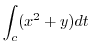 |
 |
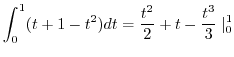 |
|
 |
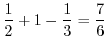 |
(b) この曲線はすでにパラメター化されている.
したがって
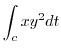 |
 |
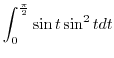 |
|
 |
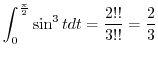 |
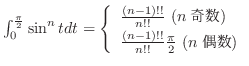
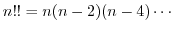 を表す.
を表す.
3. Greenの定理とは,単一閉曲線 囲まれた単連結領域
囲まれた単連結領域 上で,偏微分が連続であるような
上で,偏微分が連続であるような
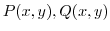 の線積分は,単連結領域
の線積分は,単連結領域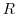 での2重積分で表せるというものである.つまり
での2重積分で表せるというものである.つまり
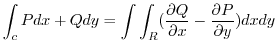
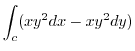 |
 |
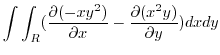 |
|
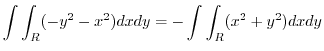 |
|||
 |
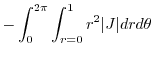 |
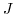 を求めると
を求めると
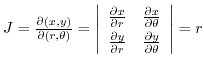 .
.
これより
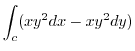 |
 |
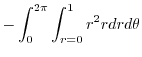 |
|
 |
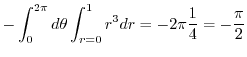 |
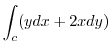 |
 |
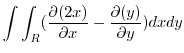 |
|
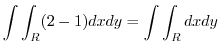 |
|||
 |
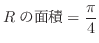 |