Next: 1.2 ドゥモワブルの定理とオイラーの公式 Up: 演習問題詳解 Previous: 演習問題詳解 索引
1.
2.
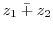 |
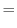 |
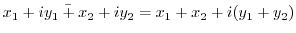 |
|
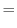 |
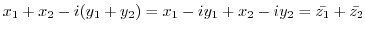 |
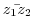 |
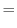 |
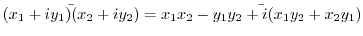 |
|
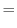 |
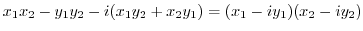 |
||
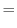 |
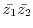 |
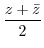 |
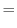 |
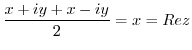 |
3.
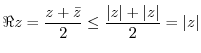
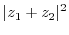 |
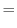 |
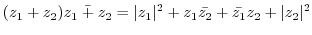 |
|
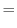 |
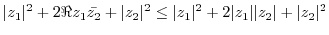 |
||
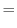 |
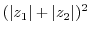 |
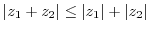
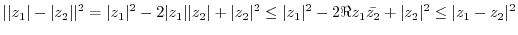
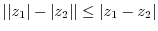
4.
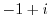 を極形式に変換するには,
を極形式に変換するには,
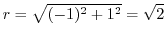 と
と
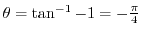 を求めればよい.これより
を求めればよい.これより
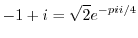
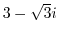 を極形式に変換するには,
を極形式に変換するには,
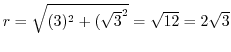 と
と
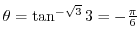 を求めればよい.これより
を求めればよい.これより
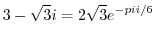
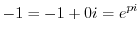
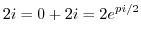
5.
(a) 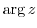 とは
とは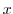 軸と原点から点
軸と原点から点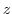 に引いた直線のなす角である.よってこれが一定ということは,点
に引いた直線のなす角である.よってこれが一定ということは,点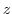 の集まりは原点から
の集まりは原点から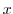 軸と一定の角をなす点となるので,直線である.
軸と一定の角をなす点となるので,直線である.
別解
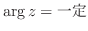 とはある定数
とはある定数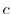 で
で
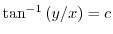 のことである.よって
のことである.よって
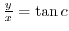 より
より
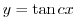 つまり,原点から放たれた直線である.
つまり,原点から放たれた直線である.
(b) 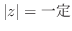 とは原点からの距離が一定のことである.したがって円を描く.
とは原点からの距離が一定のことである.したがって円を描く.
別解
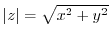 より
より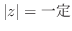 ならば,
ならば,
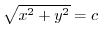 .よって
.よって
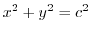 で円.
で円.
(c) 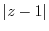 とは点1からの距離.また,
とは点1からの距離.また,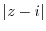 とは点
とは点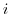 からの距離.この2つが等しい点の集まりは,点1と点
からの距離.この2つが等しい点の集まりは,点1と点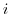 を通る垂直2等分線である.
を通る垂直2等分線である.
別解
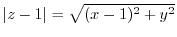 ,
,
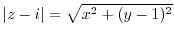 より
より
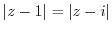 を書き直すと
を書き直すと
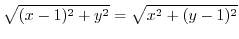
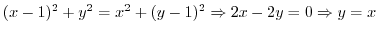
(d) 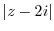 とは点2iからの距離.
よって
とは点2iからの距離.
よって
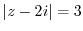 は中心
は中心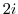 で半径が3の円を描く.
で半径が3の円を描く.
別解
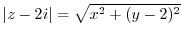 より
より
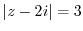 を書き直すと
を書き直すと
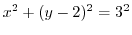
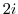 で半径が
で半径が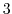 の円であることが分かる.
の円であることが分かる.
(e) 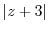 とは
とは
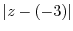 のことであるから点(-3)からの距離.
のことであるから点(-3)からの距離.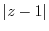 は点1からの距離.
よって
は点1からの距離.
よって
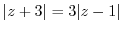 は点-3からの距離が点1からの距離の3倍になっている点
は点-3からの距離が点1からの距離の3倍になっている点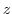 の集まり.このような点は点-3と点1を結ぶ直線を3:1に内分する点と外分する点を直径とする円を描く.この円をアポロ二ウスの円という.
の集まり.このような点は点-3と点1を結ぶ直線を3:1に内分する点と外分する点を直径とする円を描く.この円をアポロ二ウスの円という.
別解
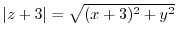 ,
,
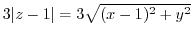 より
より
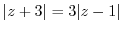 を書き直すと
を書き直すと
![$\displaystyle (x+3)^2 + y^2 = 9[(x-1)^2 + y^2]$](img234.png)
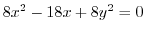
![$\displaystyle 8[(x - \frac{9}{8})^2 + y^2] = \frac{81}{8} $](img236.png)
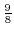 で半径が
で半径が
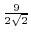 の円であることが分かる.
の円であることが分かる.