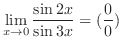Next: 3.4 解答 Up: 演習問題詳解 Previous: 3.2 解答 索引
3.3
1.
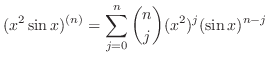
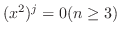 |
 |
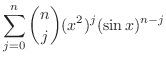 |
|
 |
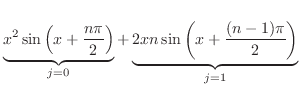 |
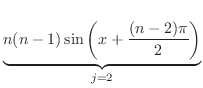
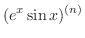
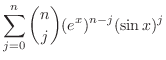
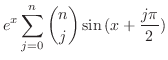
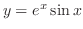
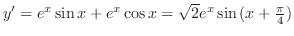
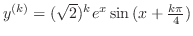
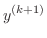
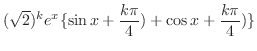
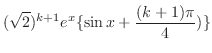
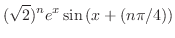 とおくと
とおくと 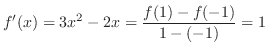 ,
,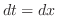 よって
よって
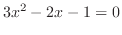
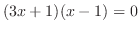
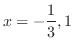
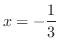 とおいて部分積分を行う
とおいて部分積分を行う
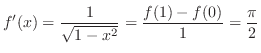
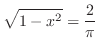 ここで部分積分をもう一度行うと
ここで部分積分をもう一度行うと
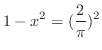
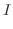 |
 |
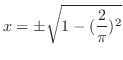 |
|
 |
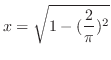 |
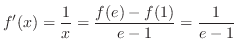 は
は
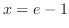
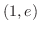
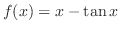
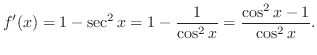
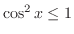
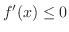
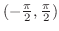
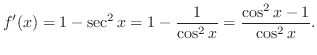
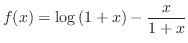
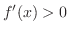
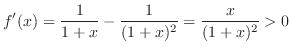 |
 |
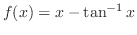 |
|
 |
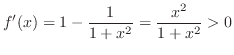 |
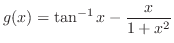
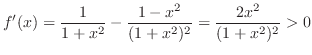
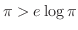 も同様に積分すると
も同様に積分すると
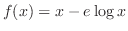
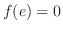
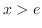 も同様に積分すると
も同様に積分すると
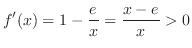
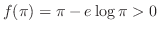
したがって