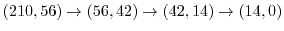Next: メソッド(method) Up: JAVA入門 Previous: 選択(selection) 目次 索引
反復(Loop)
ループとは繰り返し文のことです.俗に反復処理(iteration)と呼ばれていて構造化プログラミングの根幹をなしています.反復処理にはwhile文,do-while文とfor文があります.
その昔,コンピュータの性能が悪かった時代,また,しっかりした制御構造および反復処理がプログラミング言語に用意されたいなっかた時代,多くの人がgoto文と呼ばれるジャンプを使ってプログラムを書いていました.しかし,1960年代後半goto文によって書かれたプログラムは,他人にとってわけのわからないプログラム(スパゲッティプログラム)になり,諸悪の根源であると言われ始めました.このことより,ソフトウェアも通常の工業製品と同じように生産管理が必要であるという観点から「ソフトウェア工学」が生まれました.このような流れの中から,分かりやすいプログラムを書くための方法論がダイクストラによって提案され,その中の1つに「構造化プログラミング」があります.
構造化プログラミング(Structured Programming)
構造化プログラミングは,基本的に3つの構造から成り立っています.
|
連接(sequence):プログラムは上から下に流れる
選択構造(Selection) 反復処理(Iteration) |
構造化定理によると,すべてのアルゴリズムはこの3つの構造だけで記述できることが証明されています.
現在,Java言語を学んでいる人は,上記の1,2,3だけでアルゴリズムを書く練習をして下さい.なお,今やプロジェクトの規模が大きくなり,構造化プログラミングを用いても,ある時点からは複雑さがプログラマの管理できる限界を超えてしまっています.そこで生まれたのが,オブジェクト指向という考え方です.Java言語はすでに述べましたがオブジェクト指向言語です.
while文(while Statement):~の間~する
|
while文の構文は
while(条件式){ ステートメント; } |
の形をとります.while文は条件式が真である限り,その対象の評価を繰り返します.条件式が偽になると,ループを停止します.したがって,while文はステートメントを一つも実行せず,while文を終えることもあります.

解答 求める和をsとおくと,
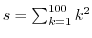 と表せます.
と表せます.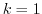 のとき,
のとき,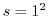 .
. 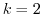 のとき,
のとき,
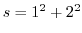 となりますが,
となりますが,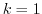 のとき,
のとき,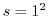 としておくと,
としておくと,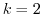 のとき,
のとき,
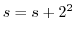 と表せることに気づいたでしょうか.これが数列の和のコーディングの方法です.
と表せることに気づいたでしょうか.これが数列の和のコーディングの方法です.
この問題では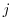 番目が
番目が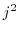 より和は
より和は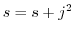 と表せます.これを
と表せます.これを が1から100まで行えばよいので,擬似コードで書くと,
が1から100まで行えばよいので,擬似コードで書くと,
j
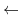 1, s
1, s
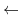 0;
0;
while (j 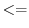 100) do
100) do
s
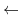 s +
s + 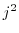 ;
;
j
 j+1;
j+1;
となります.これをJava言語に書き直すと,
|
class SumOfSquares
{
public static void main(String[] args) { int j = 1, sum = 0; while(j <= 100) { sum += j*j; j++; } System.out.println(sum); } } |
実行結果
![\begin{figure}\centering
\includegraphics[width=7.8cm]{JAVAFIG/SumOfSquares.eps}
\end{figure}](img84.png)
一般に,j番目がある関数f(j)で表せるならば,上のステートメントs += j*j;をs += f(j)と書き換えることができます..
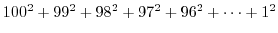 をこの順で求めるプログラムをwhileループを用いて作成しなさい. をこの順で求めるプログラムをwhileループを用いて作成しなさい.
|

解答 逆数の和をsumとし,入力された値をboundとすると,
i
 0;
0;
while(sum  bound) do
bound) do
sum
 sum + 1.0/++i;
sum + 1.0/++i;
で逆数の和が入力された値より大きくなる最初の整数iを求めることができます.Java言語に書き直すと,
|
class SumOfReciprocal
{ public static void main(String[] args) { int bound = Integer.parseInt(args[0]); int i = 0; double sum = 0.0; while(sum < bound) { sum += 1.0/++i; } System.out.println("最初の" + i + "項の逆数の和は" + sum); } } |
実行結果
![\begin{figure}\centering
\includegraphics[width=7.8cm]{JAVAFIG/SumOfReciprocal.eps}
\end{figure}](img87.png)
sum = 1 + 1/2 + 1/3 +  + 1/1000とrsum = 1/1000 + 1/999 + + 1/1000とrsum = 1/1000 + 1/999 + 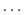 + 1をfloatで宣言し求めるプログラムを作成しなさい.sumとrsumの値を比較しなさい.また,どちらが正確か考えなさい.さらに,このとき発生した誤差はなんとよばれるか. + 1をfloatで宣言し求めるプログラムを作成しなさい.sumとrsumの値を比較しなさい.また,どちらが正確か考えなさい.さらに,このとき発生した誤差はなんとよばれるか.
|
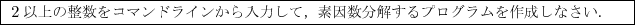
解答 素因数とは,与えられた数nの約数でかつ素数のことです.素数とは,それ自身と1でしか割れない数です.ただし,1は素数には入れません.例えば,nを120とすると,nの約数は,2,3,5であり,120の素因数分解を行なうと,
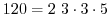 となります.
となります.
| 2 | 120 |
| 2 | 60 |
| 2 | 30 |
| 3 | 15 |
| 5 |
では,素因数分解をおこなうアルゴリズムを考えてみます.データnを読み取って,2から順に割っていき,ある数mで割れたら商n/mを新たなnとおき,さらにmで割り切れなくなるまで続ける.mで割り切れなくなったらmを1増加し,nを割っていくことを繰り返し,商nが1になるまで続ける.このとき発生した,mが素因数となります.表示するときに,最後の数字のあとには「,」を付けないようにします. では,プログラムを作成しましょう.
|
class IntFactorization
{ public static void main(String[] args) { int input = Integer.parseInt(args[0]); int divisor = 2; while(input != 1) { while(input % divisor == 0) { input /= divisor; if(input != 1) { System.out.print(divisor + "*"); } else { System.out.println(divisor); } } divisor++; } } } |
実行結果
![\begin{figure}\centering
\includegraphics[width=7.8cm]{JAVAFIG/IntFactorization.eps}
\end{figure}](img91.png)
| 与えられた数が素数かどうか判定するプログラムを作成しなさい. |
do ... while文(do ... while Statement)
|
do ... while文の構文は
do { ステートメント; }while(条件式); |
| 最低一回は必ず実行されます. |

解答
|
class SumOfSquares
{
public static void main(String[] args) { int j = 1, sum = 0; while(j <= 100) { sum += j*j; j++; } System.out.println(sum); } } |
実行結果
![\begin{figure}\centering
\includegraphics[width=7.8cm]{JAVAFIG/SumOfSqRev.eps}
\end{figure}](img93.png)
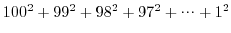 を求めるプログラムをdo...whileループを用いて作成しなさい. を求めるプログラムをdo...whileループを用いて作成しなさい.
|
階乗0!,1!,2!,3!,...は次の漸化式により定義されています.
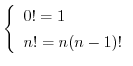
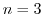 のとき,
のとき,
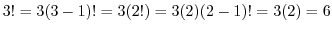
解答 階乗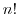 を
を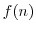 とすると,
とすると,
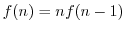 で与えられる.そこで,
で与えられる.そこで,
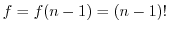 とおくと,階乗を求める構文は,繰り返しを用いて
とおくと,階乗を求める構文は,繰り返しを用いて
f = f * n
となる.この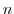 を1から順に増やしていけば,全ての階乗を求めることができる.よって,擬似コードで書くと
を1から順に増やしていけば,全ての階乗を求めることができる.よって,擬似コードで書くと
入力 bound;
i
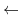 1;
1;
f
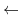 1;
1;
do
f
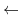 f
f 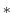 (++i);
(++i);
while(i  入力);
入力);
となる.例題5.2では再帰(recursion)を用いてn!を求めている.
|
class Factorial
{ public static void main(String[] args) { long input = Integer.parseInt(args[0]); long f = 1, i= 1; do { f *= ++i; System.out.println(f); }while(f < input); } } |
実行結果
![\begin{figure}\centering
\includegraphics[width=7.8cm]{JAVAFIG/Factorial.eps}
\end{figure}](img105.png)
for文(for Statement)
|
for文の構文は
for (初期値;条件式;更新){ ステートメント; } |
の形をとります.
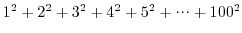 を求めるプログラムをforループを用いて作成しなさい.
を求めるプログラムをforループを用いて作成しなさい.解答
|
class SumOfSqFor
{ public static void main(String[] args) { int sum = 0; for(int j = 1; j <= 100; j++) { sum = sum + j*j; } System.out.println(sum); } } |
実行結果
![\begin{figure}\centering
\includegraphics[width=7.8cm]{JAVAFIG/SumOfSqFor.eps}
\end{figure}](img109.png)
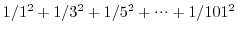 を求めるプログラムをforループを用いて作成しなさい. を求めるプログラムをforループを用いて作成しなさい.
|
実行結果
![\begin{figure}% latex2html id marker 1045
\centering
\includegraphics[width=3.3c...
...dai4-12.eps}
\includegraphics[width=3.4cm]{CPPPIC/reidai4-12-1.eps}
\end{figure}](img111.png)
解答
<実行結果1>
System.out.println("*");
で1つのアスタリスクを表示することができます.では*****と表示するにはどうすればよいでしょうか.確かにSystem.out.println("*****");でもできますが,これではアスタリスクを任意の数だけ表示せよとなると,不可能です.そこで,System.out.print("*");を5回実行すると*****が表示できることに気づけばよいでしょう.5回実行させるには,例えばforループを用いるとfor(int i=1;i =5;i++)と書けばよいことを知っています.次に,第1回目には,1つのアスタリスク,第2回目は2つのアスタリスクと増やすにはどうすればよいでしょうか.i
=5;i++)と書けばよいことを知っています.次に,第1回目には,1つのアスタリスク,第2回目は2つのアスタリスクと増やすにはどうすればよいでしょうか.i 5の5の代わりに,jを用いて,
5の5の代わりに,jを用いて,
for(int j=1;j =5;j++){
=5;j++){
for(int i=1;i =j;i++){
=j;i++){
System.out.print("*");
}
}
と書けば,外側のループが1回終了する間に内側のループがj回実行されることになります.内側のループが終了したら,"
n"で改行します.ではプログラムを作成しましょう.
|
class AstTree
{ public static void main(String[] args) { for(int j = 1; j <= 5; j++) { for(int i = 1; i <= j; i++) { System.out.print("*"); } System.out.println(); } } } |
<実行結果2>
実行結果1との違いはアスタリスクを右詰めで表示しているところです.そこで,アスタリスクの前にブランクを挿入するコマンドを追加すればよいでしょう.
|
class AstTreeRight
{ public static void main(String[] args) { for(int j = 1; j <= 5; j++) { for(int i = 1; i <= 5; i++) { if(i > 5-j) { System.out.print("*"); } else { System.out.print(" "); } } System.out.println(); } } } |
| 次のような形を表示するプログラムを作成しなさい. |
![\begin{figure}% latex2html id marker 1068
\centering
\includegraphics[width=3.0cm]{CPPPIC/renshu4-7.eps}
\end{figure}](img112.png)
continue文(continue Statement)
break文はループブロックのbreak文以下をスキップし,ループの外の次の文にジャンプします.continue文もbreak文のように,ループブロックをスキップしますが,ループを終了する代わりに,ループの次の反復に移ります.
|
class BreakAndContinue
{ public static void main(String[] args) { int n = Integer.parseInt(args[0]); for(int i = 1; i < n ; i++) { if(n % 2 == 0) { System.out.println("ループの中"); continue; } if(n % 3 == 0) { System.out.println("ループの最後"); break; } } System.out.println("ループの外"); } } |
解答 2でも3でも割り切れない数を入力すると,2つのif文の条件を満たさないので,"ループの外"が出力されます.2で割り切れる数を入力すると,"ループの中"が出力されcontinueで残りのステートメントをスキップし,ループに戻り,ループの条件が満たされなくなったら"ループの外"を出力します.2で割り切れず3で割り切れる数を入力すると,"ループの最後"を出力しbreak文でループの外に出ます.
実行結果
![\begin{figure}\centering
\includegraphics[width=7.8cm]{JAVAFIG/BreakAndContinue.eps}
\end{figure}](img113.png)
1. while文の条件式が最初から正しくない(つまり零)場合どうなるか述べなさい.
2. 次のプログラムコードはどこが間違っているか.
while (n <= 100)
sum += n*n;
3. 次のプログラムコードはどこが間違っているか.
class WhatIsWrong
{
public static void main()
{
final double PI;
int n;
PI = 3.141592653;
n = 22;
}
}
4. break文はどのようにしてループにコントロールをもたらすか述べなさい.
1. eを式,sを文とするとき,次のforループをwhileループを用いて書き直しなさい.
a. for(;e;)s
b. for ( ; ; e) s
2. 次のforループをwhileループを用いて書き直しなさい.
for (int i=1; i <= n; i++)
System.out.println(i*i + " ");
3. 次のコードをトレースしなさい.
float x = 4.15;
for (int i = 0; i  3; i++)
3; i++)
x *= 2;
4. 入力した10進数の数字を反転して出力するプログラムを書きなさい.
5. Euclidの互助法は2つの整数の最大公約数を求めるのに用いることができます.そのアルゴリズムは例えば,210と56の最大公約数ならば,
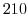 |
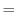 |
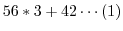 |
|
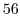 |
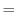 |
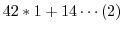 |
|
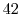 |
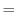 |
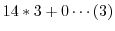 |
次に,210と56の最大公約数を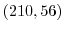 と表すと,
と表すと,