Exaple Find the fundamental matrix of the following system．

$$\left\{\begin{array}{rc} x_{1}^{\prime} =& 2x_{1} - x_{2}\\ x_{2}^{\prime} =& 4x_{1} + 6x_{2} \end{array} \right .$$

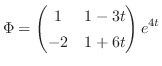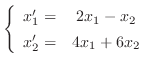
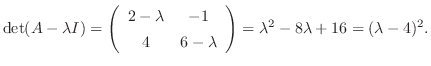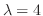Answer $\det(A - \lambda I) = \left(\begin{array}{cc} 2-\lambda&-1\\ 4&6-\lambda \end{array}\right) = \lambda^2 - 8\lambda + 16 = (\lambda - 4)^{2}.$ Then $\lambda = 4$. Next we find the eigen vector 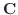${\bf C}$ corresponds to $\lambda = 4$

$$(A - 4I){\bf C} = \left(\begin{array}{cc} -2 & -1\\ 4 & 2 \end{a... ...\ c_{2} \end{array}\right) = \left(\begin{array}{c} 0\\ 0 \end{array}\right)$$

$$\left(\begin{array}{cc} -2&-1\\ 4&2 \end{array}\right) \Longrightarrow \left(\begin{array}{cc} 1&\frac{1}{2}\\ 0&0 \end{array}\right)$$

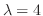
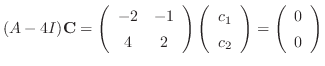
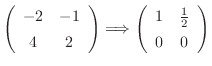
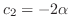Then 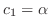we put $c_{2} = -2\alpha$. Then $c_{1} = \alpha$. Thsu the eigen vector is 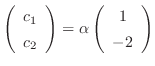$\left(\begin{array}{c} c_{1}\\ c_{2} \end{array}\right) = \alpha \left(\begin{array}{c} 1 \\ -2 \end{array}\right)$. We next find the another eigen vector corresponds to 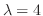$\lambda = 4$. To find so, 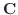${\bf C}$ must satisfies the followings:

$$(A - 4I)^2 {\bf C} = {\bf0}, \ (A - 4I){\bf C} \neq {\bf0}$$

$$(A - 4I)^2 = \left(\begin{array}{cc} -2&-1\\ 4&2 \end{array}\right)^2 = \left(\begin{array}{cc} 0&0\\ 0&0 \end{array}\right)$$

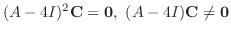
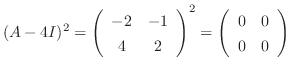
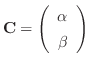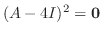Thus, if we takee ${\bf C} = \left(\begin{array}{c} \alpha\\ \beta \end{array}\right)$, $(A - 4I)^2 = {\bf0}$. Now we choose 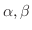$\alpha,\beta$ so that another condition is satisfied. Then 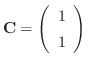${\bf C} = \left(\begin{array}{c} 1\\ 1 \end{array}\right)$ and the second eigen vector is given by

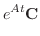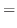$$e^{At}{\bf C} = e^{4t}e^{(A-4I)t}{\bf C} = e^{4t}[{\bf C} + t(A - 4I){\bf C} + \frac{t^2}{2!}(A - 4I)^2 {\bf C}]$$

$$= e^{4t}\{\left(\begin{array}{c} 1\\ 1 \end{array}\right) + \left(... ...array}\right)t\} = e^{4t}\left(\begin{array}{c} 1-3t\\ 1+6t \end{array}\right)$$

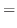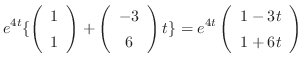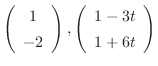ここで $\left(\begin{array}{c} 1\\ -2 \end{array}\right), \left(\begin{array}{c} 1-3t\\ 1+6t \end{array}\right)$. Note that this vector is independent. Thus, the fundamental matrix is given by the followings:

$$\Phi = \begin{pmatrix} 1 & 1-3t \\ -2 & 1+6t \end{pmatrix}e^{4t}$$