Example Find the fundamental matrix of the following system of differential equations.．

$${\bf X}^{\prime} = \left(\begin{array}{rrr} 1&-1&1\\ 1&1&-1\\ 2&-1&0 \end{array}\right){\bf X}$$

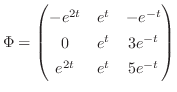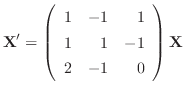
Answer

$$\det(A - \lambda I) = \left(\begin{array}{rrr} 1-\lambda&-1&1\\ ... ...\\ 2&-1&-\lambda \end{array}\right) = -(\lambda + 1)(\lambda - 1)(\lambda - 2)$$

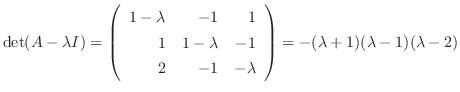
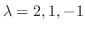Then the eigen values are $\lambda = 2, 1, -1$．Now we find the eigen vector 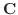${\bf C}$ corresponds to $\lambda = 2$.

$$(A - 2I){\bf C} = \left(\begin{array}{rrr} -1&-1&1\\ 1&-1&-1\\ ... ...ght)\left(\begin{array}{c} c_{1}\\ c_{2}\\ c_{3} \end{array}\right) = {\bf0}$$

Now we use Gaussian elimination)

$$A - 2I = \left(\begin{array}{rrr} -1&-1&1\\ 1&-1&-1\\ 2&-1&-2 \end{array... ...ghtarrow} \left(\begin{array}{rrr} 1&-1&1\\ 0&-2&0\\ 0&1&0 \end{array}\right)$$

$$\stackrel{\begin{array}{c} {}_{R_{2} \leftrightarrow R_{3}}\\ {}... ..._{3}+R_{2}\to R_{2}}\\ {}_{R_{3}+R_{1}\to R_{1}} \end{array}}{\longrightarrow} \left(\begin{array}{rrr} 1&0&1\\ 0&1&0\\ 0&0&0 \end{array}\right)$$

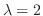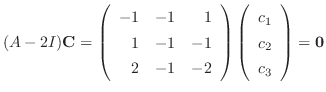
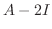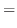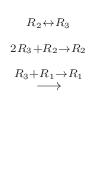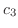Here $c_{3}$ is an arbitrary constant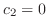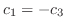，$c_{2} = 0$, $c_{1} = -c_{3}$. Then the vector C is represented by 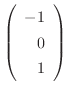$\left(\begin{array}{r} -1\\ 0\\ 1 \end{array}\right)$, where 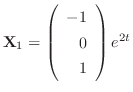${\bf X}_{1} = \left(\begin{array}{r} -1\\ 0\\ 1 \end{array}\right)e^{2t}$ is an answer．
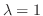For the eigen value $\lambda = 1$, we find the eigen vector.

$$A - I = \left(\begin{array}{rrr} 0&-1&1\\ 1&0&-1\\ 2&-1&-1 \end{array}\... ...htarrow} \left(\begin{array}{rrr} 1&0&-1\\ 0&-1&1\\ 0&-1&1 \end{array}\right)$$

$$\stackrel{\begin{array}{c} {}_{-1 \times R_{2}\to R_{2}} \\ {}_{-R_{2}+R_{3}\to R_{3}} \end{array}}{\longrightarrow} \left(\begin{array}{rrr} 1&0&-1\\ 0&1&-1\\ 0&0&0 \end{array}\right)$$

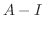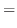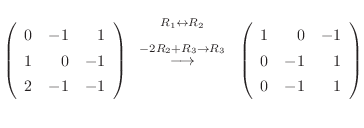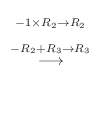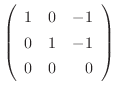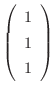Then the eigen vector is $\left(\begin{array}{r} 1\\ 1\\ 1 \end{array}\right)$. Thus, 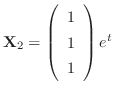${\bf X}_{2} = \left(\begin{array}{r} 1\\ 1\\ 1 \end{array}\right)e^{t}$ is also a solution．Similarly, we find the eigen vector corresponding to $\lambda = -1$.

$$A + I = \left(\begin{array}{rrr} 2&-1&1\\ 1&2&-1\\ 2&-1&1 \end{array}\r... ...htarrow} \left(\begin{array}{rrr} 1&2&-1\\ 0&-5&3\\ 0&-5&3 \end{array}\right)$$

$$\stackrel{\begin{array}{c} {}_{-\frac{1}{5} \times R_{2}\to R_{2}... ... R_{3}}\\ {}_{\frac{2R_{2}}{5} + R_{1}\to R_{1}} \end{array}}{\longrightarrow} \left(\begin{array}{rrr} 1&0&1/5\\ 0&1&-3/5\\ 0&0&0 \end{array}\right)$$

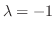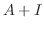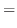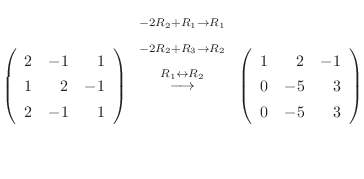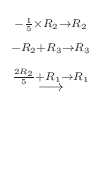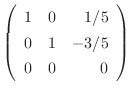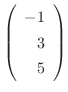Then the eigen vector is $\left(\begin{array}{r} -1\\ 3\\ 5 \end{array}\right)$. This shows that 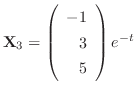${\bf X}_{3} = \left(\begin{array}{r} -1\\ 3\\ 5 \end{array}\right)e^{-t}$ is also a solution．Now 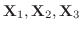${\bf X}_{1},{\bf X}_{2},{\bf X}_{3}$ are independent. Thus,the general solution is given by

$${\bf X} = c_{1}\left(\begin{array}{r} -1\\ 0\\ 1 \end{array}\ri... ...ight)e^{t} + c_{3}\left(\begin{array}{r} -1\\ 3\\ 5 \end{array}\right)e^{-t}$$

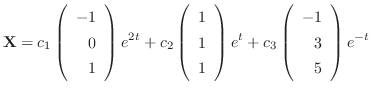
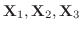Here the matrix composed by column vectors ${\bf X}_{1},{\bf X}_{2},{\bf X}_{3}$ is the fundamental matrix.

$$\Phi = \begin{pmatrix} -e^{2t} & e^{t} & -e^{-t}\\ 0 & e^{t} & 3e^{-t}\\ e^{2t} & e^{t} & 5e^{-t} \end{pmatrix}$$