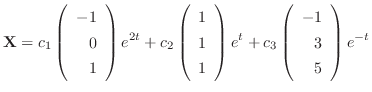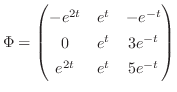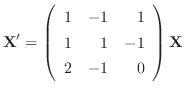
解答
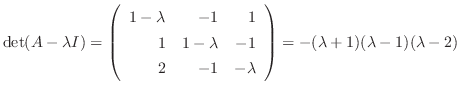
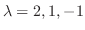 である.次に固有値
である.次に固有値
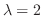 に対する固有ベクトル
に対する固有ベクトル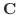 は
は
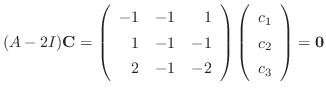
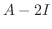 |
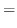 |
 |
|
 |
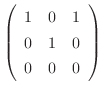 |
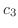 は任意の定数,
は任意の定数,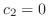 ,
,
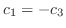 となる.したがって,固有ベクトルCは
となる.したがって,固有ベクトルCは
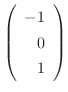 で表わされ,
で表わされ,
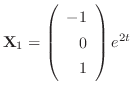 はこの微分方程式のひとつの解である.
はこの微分方程式のひとつの解である.
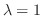 に対する固有ベクトルは
に対する固有ベクトルは
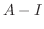 |
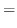 |
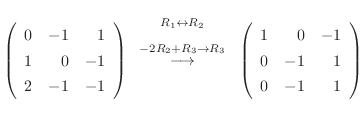 |
|
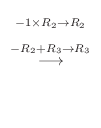 |
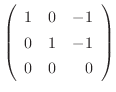 |
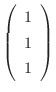 で表わされ,
で表わされ,
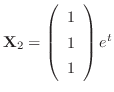 もこの微分方程式のひとつの解である.同様に固有値
もこの微分方程式のひとつの解である.同様に固有値
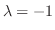 に対する固有ベクトルは
に対する固有ベクトルは
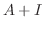 |
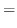 |
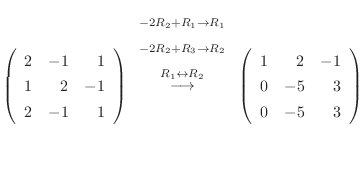 |
|
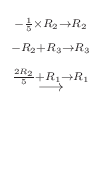 |
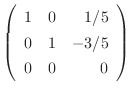 |
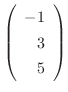 で表わされ,
で表わされ,
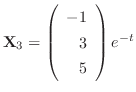 もこの微分方程式のひとつの解である.ここで
もこの微分方程式のひとつの解である.ここで
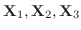 は一次独立なので
は一次独立なので
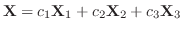 は一般解になると思われる.次の定理で述べるが,確かにこれは一般解である.よって一般解は
は一般解になると思われる.次の定理で述べるが,確かにこれは一般解である.よって一般解は