配列
配列の概念
先に断っておくが、C言語では、配列は次章で学ぶポインタとの間に強い関係があるので、配列はポインタと一緒に学ぶことを勧める。
プログラムを作るときには、データを変数という箱に入れて、これに変数名という名前を付けて扱った。しかし、この方法では、プログラムを作る上で非常に困難になることがある。
例題6.1 6段の引き出しに科目別の受講生の数が次のように入っていたとする。
|
段数 |
1 |
2 |
3 |
4 |
5 |
6 |
|
内容 |
微分学 |
積分学 |
線形代数 |
C++言語 |
数値解析 |
応用数学 |
|
数量 |
95 |
100 |
55 |
80 |
60 |
40 |
ここで、キーボードから引き出しの段数を表す数を入力し、その内容物の数量を表示するプログラムを作成しよう。例えば、3と入力した場合には3段目の積分学の受講生の数55を表示し、4と入力した場合には4段目のC++言語の受講生の数80を表示する。
実行例
そこで、1段目をdrower1、2段目をdrower2、とおくと,、プログラムは
|
#include <stdio.h> void main(void) { int drower1 = 95; int drower2 = 100; int drower3 = 55; int drower4 = 80; int drower5 = 60; int drower6 = 40; int i; scanf(“%d”,&i); if (i == 1) { printf(“%d”,drower1); } else if (i == 2) { printf(“%d”,drower2); } else if (i == 3) { printf(“%d”,drower3); } else if (i == 4) { printf(“%d”,drower4); } else if (i == 5) { printf(“%d”,drower5); } else { printf(“%d”,drower6); } } |
となる。このプログラムでは、個々の場合を記述せねばならず、複雑で長くなる。もし、これが、大学全体の受講生となると、引出しの数が100や200では足りなくなってしまう。たとえ、これらの変数を個々に定義して表示できたとしても、長くて見通しの悪いプログラムになってしまうだろう。
そこで、このような場合に用いるものに、配列(array)というものがある。配列は「何番目のデータ」という表現ができる変数である。ベクトルや行列を配列を用いて表現することもできる。
1次元配列を用いるためには、変数を配列として定義する必要がある。例えば、
int drower[6];
とすると、drowerという配列を用意し、そこには6個のデータが格納できることを意味する。このように定義すると、drower[0],drower[1],…,drower[5]の合計6個の変数が用意される。これより上のプログラムをもう一度書き直すと
|
#include <stdio.h> void main(void) { int i; int drower[6]; int choice=0;
drower[1] = 95; drower[2] = 100; drower[3] = 55; drower[4] = 80; drower[5] = 60; drower[6] = 40; do { choice=1; printf("数字を入力してください\n"); scanf("%d",&i); if((i <=0) || (i > 6)) { printf("1から6までの数字を入力してください\n"); } else { printf("%d\n",drower[i-1]); } printf("続けたければ0を入力"); scanf("%d",&choice); } while (choice==0); } |
となる。このプログラムでは、個々の場合を記述せねばならず、複雑で長くなる。もし、これが、大学全体の受講生となると、引出しの数が100や200では足りなくなってしまう。たとえ、これらの変数を個々に定義して表示できたとしても、長くて見通しの悪いプログラムになってしまうだろう。
そこで、このような場合に用いるものに、配列(array)というものがある。配列は「何番目のデータ」という表現ができる変数である。ベクトルや行列を配列を用いて表現することもできる。
1次元配列を用いるためには、変数を配列として定義する必要がある。例えば、
int drower[] =
{95,100,55,80,60,40};
とすると、drowerという配列を用意し、そこには6個のデータが格納できることを意味する。このように定義すると、drower[0],drower[1],…,drower[5]の合計6個の変数が用意される。これより上のプログラムをもう一度書き直すと
#include <stdio.h>
void main(void)
{
int i;
int drower[6] = {95,100,55,80,60,40};
int choice=0;
do
{
choice=1;
printf("数字を入力してください\n");
scanf("%d",&i);
if((i <=0) || (i > 6))
{
printf("1から6までの数字を入力してください\n");
}
else
{
printf("%d\n",drower[i-1]);
}
printf("続けたければ0を入力");
scanf("%d",&choice);
} while (choice==0);
}
2つの添え字をもつ配列を2次元配列という。例えば、
int data[3][2] = {1,2,3,4,5,6};
とすると、dataという配列を用意し、そこには3かける2、つまり6個のデータが格納できることを意味する。これは、data[0][0]=1;data[0][1]=2;data[1][0]=3;data[1][1]=4;data[2][0]=5;data[2][1]=6;と代入を行ったのと同じことである。
配列を用いる基準
配列を用いずにプログラムが組めるのであれば、配列を使わない。
配列を用いるのは、データを蓄えておいて、後で再利用する場合や、そのデータの各要素をランダムに参照する場合などである。
練習問題6.1 プログラムの中の括弧および□を埋めて、素因数分解のプログラムを完成せよ。アルゴリズムとしてはもとの数値を小さい素数から順に割っていき、その割った商が1になるまで繰り返せばよい。
#include <stdio.h>
#define N_MAX 32768
int flg[N_MAX];
void main(void)
{
int i,j,n;
printf(“データを入力してください”);
scanf(“%d”,&n);
for(i=2; i <=N_MAX; i++)
flg[i] = 1;
for(i=2; i < N_MAX && n! = 1; i++)
{
if (flg[i]){
while(ア ==0) {
printf(“%5d”,i);
|
イ |
}
for(j = 2*i;j < N_MAX; j+=i)
flg[j] = 0;
}
}
}
解答 すでに見つけた約数の倍数以外の中から、新しい約数を検出するプログラムである。約数である条件は、余りが0のことである。よってアにはn%iが入りイにはn/=iが入る。
|
n/=iとはn=n/iのことである。他にもn+=1はn=n+1またはn++と表せる。 |
例題6.2 もう一つ配列の問題を考えてみよう。
次の表は広島工業大学のある科目の期末テストの点数である。データは30人分ある。このデータを入力して、平均値、分散、標準偏差を計算するプログラムを作成してみよう。
|
60 80 70 85 90 45 60 70 55 60 70 80 70 75 80 95 60 40 50 60 70 80 60 70 50 70 80 90 60 70 |
実行結果
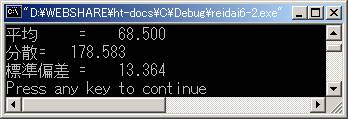
考え方
これらのデータをdj、j=1,2,…30に格納する。平均mean、分散variance、標準偏差std_devは次の式で表せることに注意する。
![]()
この式に基づいて作成したプログラムは次のようになる。
まず、データを格納する配列をdeta[30]とする。データを順に読み込むにはfor(i=0;i<=29;i++)と配列は0から始まることに注意する。また、平方根を求めるためにsqrt関数を用いるので、math.hをインクルードしておく。
解答
|
#include <stdio.h> #include <math.h> void main(void) { int data[30]; double mean,variance,std_dev; int i,n = 30; double sum; for (i = 0;i < n; i++) { printf("%d番目のdata = ", i+1); scanf("%d",&data[i]); } for (sum = 0.0,i = 0;i < n; i++) { sum = sum + data[i]; } mean = sum/n; for( sum = 0.0,i = 0;i < n;i++) { sum = sum + (data[i] - mean)*(data[i] - mean); } variance = sum/n; std_dev = sqrt(variance);
printf("平均 =%10.3f\n",mean); printf("分散=%10.3f\n",variance); printf("標準偏差 =%10.3f\n",std_dev); } |
2次元配列を用いた行列の計算
2次元配列は、行列計算としての使い道が非常に多い。例えば、n行m列の行列は、次のように定義する。n=4,m=5とすると
float matrix[4][5];
または、マクロ名を用いて
#define LOW 4
#define COLUMN 5
float matrix[LOW][COLOMN];
としたほうがさらによい。
配列では、確保する記憶量が多くなる。2次元配列では、さらに多くの領域を必要とする。例えば、4行5列の2次元配列では20個の要素が必要で、ここでは要素の型がfloat形なので、20×4バイト →80バイトの領域が必要となる。double型にすると、20×8バイト → 160バイトの領域が必要になる。このこのことから、配列の型は、必要とする精度を考慮してなるべく確保する領域の小さい型を選ぶべきである。
例題6.3 行列の加算
次のような4行3列の行列の和を求めるプログラムを作成してみよう。
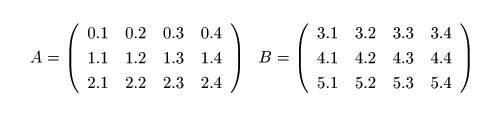
実行例
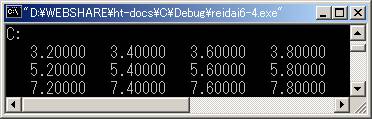
考え方
行列A、Bは次のように定義できる。
float a[4][3], b[4][3];
または、マクロ名を用いて
#define LOW3
#define COLUMN 4
とも定義できる。後々のことを考えるとマクロ名を用いて定義しておくほうがよい。
まず、行列Aの成分を読み込む。行と列があるので、ダブルループを作る。行ごとに読み込むには、外側のループが行で内側のループが列となる。つまり
for (i=0;i < LOW; i++)
{
for (j=0;j < COLUMN;j++)
{
printf(“A[%d,%d]=”,i+1,j+1);
scanf(“%f”,&a[i][j]);
}
}
と書くと1行目に対して、1列目から4列目までを読み込むことになる。
準備はこのくらいにして、プログラムを書いてみよう。
解答
|
#include <stdio.h> #define LOW 3 #define COLUMN 4 void main(void) { float a[LOW][COLUMN]; float b[LOW][COLUMN]; float c[LOW][COLUMN]; int i,j;
for (i = 0;i < LOW; i++) { for (j = 0;j < COLUMN;j++) { printf("A[%d][%d]=",i+1,j+1); scanf("%f",&a[i][j]); } } for (i = 0;i < LOW; i++) { for (j = 0;j < COLUMN;j++) { printf("B[%d][%d]=",i+1,j+1); scanf("%f",&b[i][j]); } } for (i = 0;i < LOW; i++) { for (j = 0;j < COLUMN;j++) { c[i][j] = a[i][j] + b[i][j]; } } printf("\nC:\n"); for (i = 0;i < LOW; i++) { for (j = 0;j < COLUMN;j++) { printf("%10.5f",c[i][j]); } printf("\n"); } } |
例題6.4 行列の積
ついでにもう1つの例を示す。これは次の行列の積を求めるプログラムである。
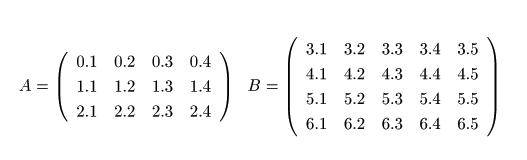
実行結果
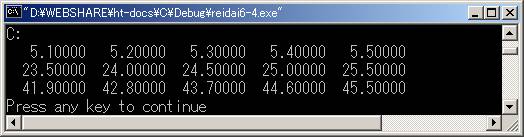
考え方
行列の積はC=ABのとき、Cのij成分は
![]()
で求まることに注意する。これは和である。和の求め方は(s=s+f(j))であるので、
C[i][j] = 0;
C[i][j] = C[i][j] + a[i][k]*b[k][j];
でC[i][j]が求まる。では、プログラムを書いてみよう。
解答
|
#include <stdio.h> #define ROW_A 3 #define COLUMN_A 4 #define ROW_B 4 #define COLUMN_B 5 void main(void) { float a[ROW_A][COLUMN_A]; float b[ROW_B][COLUMN_B]; float c[ROW_A][COLUMN_B]; int i,j,k;
for (i = 0;i < ROW_A; i++) { for (j = 0;j < COLUMN_A;j++) { printf("A[%d][%d]=",i+1,j+1); scanf("%f",&a[i][j]); } } for (i = 0;i < ROW_B; i++) { for (j = 0;j < COLUMN_B;j++) { printf("B[%d][%d]=",i+1,j+1); scanf("%f",&b[i][j]); } } for (i = 0;i < ROW_A; i++) { for (j = 0;j < COLUMN_B;j++) { c[i][j] = 0; for (k=0;k < ROW_B;k++) { c[i][j] = c[i][j] + a[i][k] * b[k][j]; } } } printf("\nC:\n"); for (i = 0;i < ROW_A; i++) { for (j = 0;j < COLUMN_B;j++) { printf("%10.5f",c[i][j]); } printf("\n"); } } |